《2025年拔尖特训五年级数学上册人教版》

1. 填表。

2.2554.53

答案： 解析：本题主要考查三角形和平行四边形的面积公式。
三角形面积公式为$S=\frac{1}{2}×底×高$，
平行四边形面积公式为$S = 底×高$。
对于三角形，已知底是$3cm$，高是$1.5cm$，
根据公式可得面积$S_1=\frac{1}{2}×3×1.5 = 2.25cm^{2}$；
又已知一个三角形面积为$7.5cm^{2}$，底是$3cm$，
由公式变形可得高$h_2 = 7.5×2÷3=5cm$。
对于平行四边形，已知底是$3cm$，高是$1.5cm$，
根据公式可得面积$S_3 = 3×1.5 = 4.5cm^{2}$；
已知底是$5.2cm$，面积是$15.6cm^{2}$，
由公式变形可得高$h_4=15.6÷5.2 = 3cm$。
答案：2.25；5；4.5；3。

(1)一个三角形和一个平行四边形的面积相等,高也相等,如果三角形的底是16 cm,那么平行四边形的底是(A)cm。
A.8
B.16
C.32
D.无法确定

答案： 解析：本题主要考查三角形和平行四边形的面积公式。
三角形的面积公式是：$面积 = \frac{1}{2} × 底 × 高$，
平行四边形的面积公式是：$面积 = 底 × 高$，
已知三角形和平行四边形的面积相等，且高也相等，三角形的底是$16 cm$。
设平行四边形的高为$h$，底为$b$，三角形的底为$16 cm$，高也为$h$。
根据面积相等，可以列出等式：
$\frac{1}{2} × 16 × h = b × h$，
两边同时除以$h$（因为$h$不为$0$）：
$\frac{1}{2} × 16 = b$，
解得：$b = 8$。
所以，平行四边形的底是$8 cm$。
答案：A.8。

(2)公园有一块长20 m、宽16 m的长方形空地。下面是美化空地的几种设计方案,其中涂色部分种鲜花,空白部分铺草坪。这些方案中,种鲜花的面积是$160 m^2$的有(C)种。
A. 1
B. 2
C. 3
D. 4

答案： 解析：本题主要考查长方形和三角形的面积公式。
第一种方案：
长方形面积公式为$S = a × b$，其中$a$为长，$b$为宽。
已知长方形空地长$20m$、宽$16m$，则长方形空地面积为$20×16 = 320(m^2)$。
涂色部分是两个三角形，且这两个三角形的高之和为长方形的宽，底为长方形的长。
根据三角形面积公式$S = \frac{1}{2} × a × h$（$a$为底，$h$为高），可得涂色部分面积为$2×\frac{1}{2}×20×16×\frac{1}{2}= 160(m^2)$（因为两个三角形的高之和为$16m$，可看作每个三角形高为$16m$的一半，底都是$20m$）。
第二种方案：
涂色部分是三个三角形，这三个三角形的底之和为长方形的长，高为长方形的宽。
三个三角形面积之和为$\frac{1}{2}×20×16×\frac{1}{2}×2+\frac{1}{2}×20×16×\frac{1}{2}×\frac{1}{2}=160 + 40 = 200(m^2)\neq160(m^2)$。
第三种方案：
涂色部分可看作两个三角形，这两个三角形的底都是长方形的长，高之和为长方形的宽。
其面积为$2×\frac{1}{2}×20×(16÷2)= 160(m^2)$。
第四种方案：
涂色部分是四个三角形，每个三角形的底为$20÷2 = 10(m)$，高为$16÷2 = 8(m)$。
一个三角形面积为$\frac{1}{2}×10×8 = 40(m^2)$，四个三角形面积为$4×40 = 160(m^2)$。
经计算，第一种、第三种、第四种方案种鲜花的面积是$160m^2$，共$3$种。
答案：C。

3.(生物百科)“菌光互补”,即在木耳大棚的顶部安装光伏板,是农民提高木耳产量的“绿色法宝”。下面是一个三角形木耳大棚(单位：米),边BC上的高是多少？

答案： 解析：本题考查三角形面积公式。
已知$S_{\bigtriangleup ABC}$，底边$BC$长度，可利用面积公式求出$BC$边上的高。
三角形面积公式为$S=\frac{1}{2}× a × h$（$a$为底边长，$h$为这条底边对应的高）。
先根据已知的底$AC = 24$米和高$11.52$米求出三角形面积，再根据面积和底$BC = 14.4$米求出$BC$边上的高。
$S_{\bigtriangleup ABC}=\frac{1}{2}× 24× 11.52 = 138.24$（平方米）。
设边$BC$上的高为$h$米。
由$S_{\bigtriangleup ABC}=\frac{1}{2}× BC× h$，
可得$138.24=\frac{1}{2}× 14.4× h$。
则$h = 138.24× 2÷14.4=19.2$（米）。
答案：19.2米。

4. 方格纸上有一个三角形DBC,点D的位置用数对表示为(x,4)。试比较三角形ABC的面积和三角形DBC的面积的大小,并说明理由。

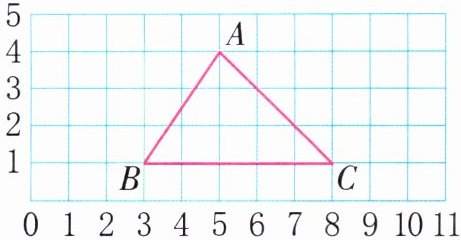
答案： 解析：本题考查三角形面积比较，关键在于明确两个三角形与方格纸的关系，通过分析它们底和高的关系来判断面积大小。
从图中可知，三角形$ABC$和三角形$DBC$的高都是点$D$或点$A$到$BC$的垂直距离，这个距离是固定的，因为点$D$和点$A$在同一水平线上（纵坐标都是$4$），$BC$在同一水平线上（纵坐标都是$1$），所以它们的高相等。
三角形$ABC$的底是线段$BC$，三角形$DBC$的底同样是线段$BC$，所以两个三角形的底也相等。
根据三角形面积公式$S = \frac{1}{2}ah$（其中$a$是底，$h$是高），由于两个三角形等底等高，所以它们的面积相等。
答案：三角形$ABC$的面积和三角形$DBC$的面积相等。理由：三角形$ABC$和三角形$DBC$有相同的底$BC$，且它们的高都是点$D$或点$A$到$BC$的垂直距离，等底等高的三角形面积相等。

5. 如图,一个平行四边形被分成两个三角形,其中一个三角形的面积是$8.4 dm^2,$这个平行四边形的周长是多少分米？

答案： 平行四边形面积：8.4×2=16.8(dm²)
一条边长：16.8÷3.5=4.8(dm)
另一条边长：16.8÷4=4.2(dm)
周长：(4.8+4.2)×2=18(dm)
答：这个平行四边形的周长是18分米。

6.(思维过程)如图,平行四边形的面积是96平方厘米,它的底被平均分成3份,涂色部分的面积是多少平方厘米？

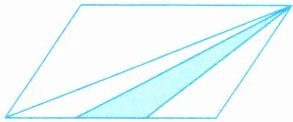
答案： 解析：本题考查平行四边形和三角形的面积计算。
已知平行四边形的面积是$96$平方厘米，它的底被平均分成$3$份，
观察图片可知，涂色部分是一个三角形，它的底是平行四边形底边长度的$\frac{1}{3}$，高等于平行四边形的高。
根据三角形的面积公式：
$面积 =\frac{1}{2} × 底 × 高$，
平行四边形的面积公式：
$面积 =底 × 高$，
可知，涂色三角形的面积是等底等高平行四边形面积的$\frac{1}{2} × \frac{1}{3} =\frac{1}{6}$，
所以，涂色部分的面积为：
$96 × \frac{1}{6}=16(平方厘米)$。
答案：涂色部分的面积是$16$平方厘米。