《2025年拔尖特训五年级数学上册人教版》

1.(算理理解)填空。
(1)如图,两个(完全相同)的三角形可以拼成一个平行四边形,因为平行四边形的面积= (底×高),所以三角形的面积= (底×高÷2),用字母表示为$ S= $($ ah÷2 $)。
(2)三角形的面积是与它等底等高的平行四边形面积的(一半)。

答案：
(1)完全相同　底×高　底×高÷2 $ ah÷2 $
(2)一半

2. 选择合适的数据计算下面三角形的面积。(单位：厘米)
(1)
(2)

答案：
(1)$ 3×4÷2=6 $（平方厘米）或 $ 5×2.4÷2=6 $（平方厘米）　
(2)$ 11.2×6÷2=33.6 $（平方厘米）解析:题图中有多个数据，选择相对应的底和高进行计算。

3. 有一个三角形花圃,底是 25 米,高是 22 米。若每平方米种鲜花 20 株,则这个花圃一共可以种鲜花多少株?

答案： $ 25×22÷2=275 $（平方米）$ 275×20=5500 $（株）

4. 在下面的方格纸中画出面积都是$ 3\ \text{cm}^2 $的锐角三角形、直角三角形和钝角三角形。(每个小方格的边长都表示1 cm)

答案：
答案不唯一,如　　

5.(几何直观)如图,平行四边形的面积是$ 40.5\ \text{cm}^2 $,求涂色三角形的面积。

答案： $ 40.5÷4.5=9 $（cm） $ 9-7=2 $（cm）$ 2×4.5÷2=4.5 $（$ \text{cm}^2 $）解析:先根据平行四边形的面积和高，求出平行四边形的底是 $ 40.5÷4.5=9 $（cm），那么涂色三角形的底是 $ 9-7=2 $（cm），再结合涂色三角形的高等于平行四边形的高，求出涂色三角形的面积。

6.(思维过程)如图,在直角梯形中,阴影三角形BCE与阴影三角形ADE的面积相差多少平方厘米?

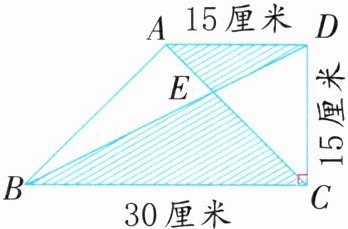
答案： 三角形BCD的面积:$ 30×15÷2=225 $（平方厘米）三角形ADC的面积:$ 15×15÷2=112.5 $（平方厘米）阴影三角形的面积差:$ 225-112.5=112.5 $（平方厘米）解析:两个阴影三角形的高是未知的，因此无法直接求出它们的面积。观察题图可知，三角形BCE+三角形CED=三角形BCD，三角形ADE+三角形CED=三角形ADC，所以阴影三角形BCE与阴影三角形ADE的面积差就是三角形BCD与三角形ADC的面积差。分别求出三角形BCD与三角形ADC的面积，再相减即可。