第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1.(算理理解)看图填空。
(1)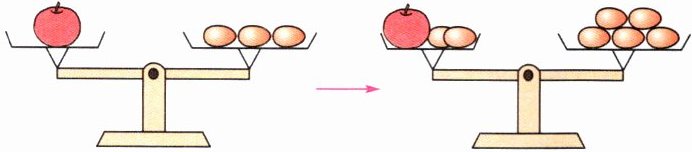
一个苹果和(

天平两边都拿走一只鹅,天平仍然(

等式的性质1:等式两边加上或减去(
(2)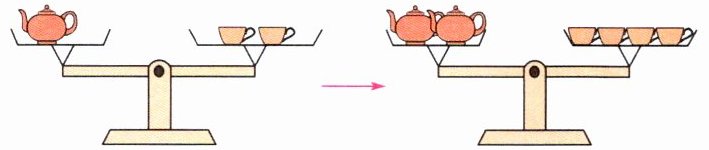
两边物品的数量同时扩大到原来的2倍,天平仍然(
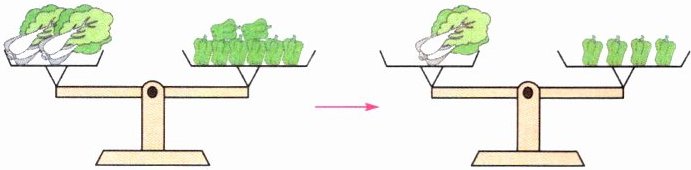
两边蔬菜数量同时减少一半,天平仍然(

等式的性质2:等式两边乘同一个数,或除以同一个(
(1)

一个苹果和(
3
)个鸡蛋一样重。两边同时各加上2个鸡蛋,天平保持(平衡
)。
天平两边都拿走一只鹅,天平仍然(
平衡
),此时一只鹅和(3
)只鸡一样重。
等式的性质1:等式两边加上或减去(
同一个数
),左右两边仍然(相等
)。(2)

两边物品的数量同时扩大到原来的2倍,天平仍然(
平衡
)。
两边蔬菜数量同时减少一半,天平仍然(
平衡
)。
等式的性质2:等式两边乘同一个数,或除以同一个(
不为0
)的数,左右两边仍然(相等
)。
答案:
1.
(1)3 平衡 平衡 3 同一个数 相等
(2)平衡 平衡 不为0 相等
(1)3 平衡 平衡 3 同一个数 相等
(2)平衡 平衡 不为0 相等
(1)如果$x= y$,根据等式的性质,经过变换后下面(
A.$6x= 6y$
B.$x÷ b= y÷ b$($b$不为0)
C.$x+8= y+10-2$
D.$x-8= y-6+2$
D
)是错误的。A.$6x= 6y$
B.$x÷ b= y÷ b$($b$不为0)
C.$x+8= y+10-2$
D.$x-8= y-6+2$
答案:
(1)D
(1)D
(2)(算法探究)已知$17+3x= 26$,则下面变换正确的是(
A.$17-17+3x= 26+17$
B.$17+3x-3x= 26-17$
C.$17+3x-17= 26-17$
D.$17+3x-17= 26-10+7$
C
)。A.$17-17+3x= 26+17$
B.$17+3x-3x= 26-17$
C.$17+3x-17= 26-17$
D.$17+3x-17= 26-10+7$
答案:
(2)C
(2)C
3. 在〇里填上合适的运算符号,在□里填上合适的数,使天平平衡。
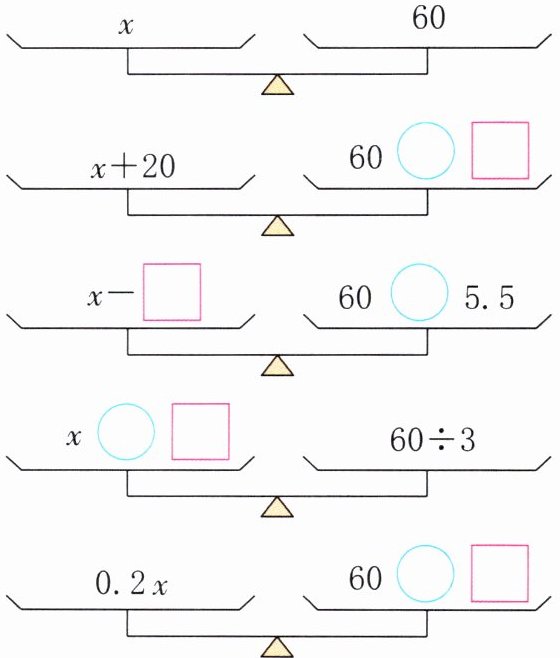

+
20
5.5
−
÷
3
×
0.2
答案:
+ 20 5.5 − ÷ 3 × 0.2
4. 根据等式的性质,把下面的等式填写完整。
(1)$5a= b$
$5ac=$
(2)$a+b+10= c+a$
(3)$m+n= q$
$2m+n=$
(4)$20ab= 5ac$($a$不为0)
$4b=$
(1)$5a= b$
$5ac=$
b
×c
(2)$a+b+10= c+a$
b
+10
$=c$(3)$m+n= q$
$2m+n=$
q
+m
(4)$20ab= 5ac$($a$不为0)
$4b=$
c
答案:
4.
(1)b c 解析:等式两边同时乘c。
(2)b 10 解析:等式两边同时减a。
(3)q m 解析:等式两边同时加m。
(4)c 解析:等式两边同时除以5a(a不为0)。
(1)b c 解析:等式两边同时乘c。
(2)b 10 解析:等式两边同时减a。
(3)q m 解析:等式两边同时加m。
(4)c 解析:等式两边同时除以5a(a不为0)。
5.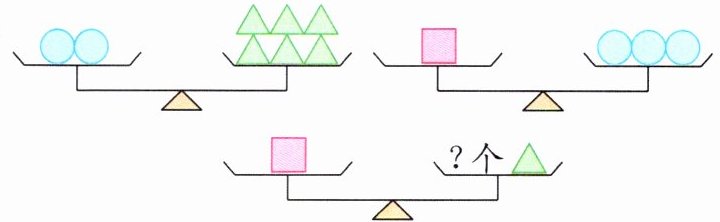
图中“?”处应该填( );如果△= 3.6,那么○= ( ),□= ( )。

图中“?”处应该填( );如果△= 3.6,那么○= ( ),□= ( )。
答案:
5.9 10.8 32.4 解析:由第一幅题图可知,1个 相当于3个
相当于3个 ,由第二幅题图可知,1个
,由第二幅题图可知,1个 相当于3个
相当于3个 ,所以1个
,所以1个 相当于9个
相当于9个
5.9 10.8 32.4 解析:由第一幅题图可知,1个
 相当于3个
相当于3个 ,由第二幅题图可知,1个
,由第二幅题图可知,1个 相当于3个
相当于3个 ,所以1个
,所以1个 相当于9个
相当于9个
查看更多完整答案,请扫码查看


