第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 把下面各组合图形分割成已学过的规则图形。
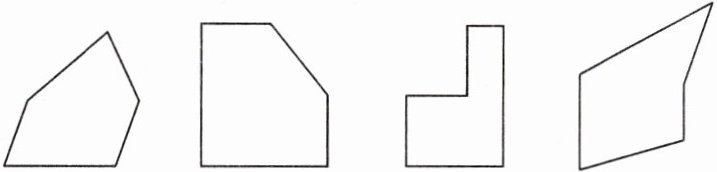

答案:
分割方法不唯一,如:
分割方法不唯一,如:

2. 下图中,长方形的面积是 $ 80 \mathrm{cm}^{2} $,涂色部分的面积是(
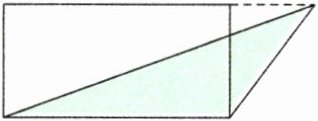
A.30
B.40
C.50
D.60
B
)$ \mathrm{cm}^{2} $。
A.30
B.40
C.50
D.60
答案:
B
3. 下图是由一个大正方形与一个小正方形拼成的,已知小正方形的边长为 $ 5 \mathrm{cm} $,涂色部分的面积为 $ 45 \mathrm{cm}^{2} $,则空白部分的面积为(
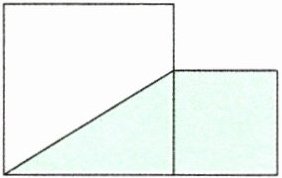
A.20
B.30
C.35
D.44
D
)$ \mathrm{cm}^{2} $。
A.20
B.30
C.35
D.44
答案:
D 【提示】根据已知条件先求出大正方形的边长为$(45-5× 5)÷ 5=8(\text{cm})$,再利用梯形面积公式求出空白部分梯形的面积为$(8-5+8)× 8÷ 2=44(\text{cm}^2)$。
4. 求下面各图形中涂色部分的面积。(单位:cm)
(1)
(2)
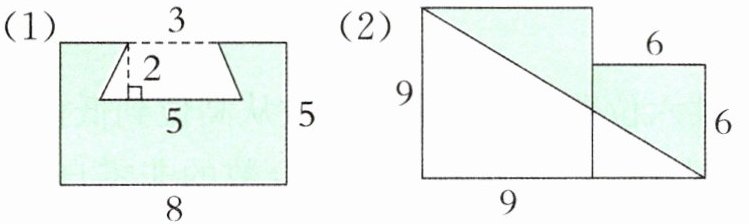
(1)
(2)

答案:
(1)$8× 5-(3+5)× 2÷ 2=32(\text{cm}^2)$
(2)$(9× 9+6× 6)-9× (9+6)÷ 2=49.5(\text{cm}^2)$
【提示】观察图形,利用图形的面积公式求出答案。
(1)$8× 5-(3+5)× 2÷ 2=32(\text{cm}^2)$
(2)$(9× 9+6× 6)-9× (9+6)÷ 2=49.5(\text{cm}^2)$
【提示】观察图形,利用图形的面积公式求出答案。
5. 一块梯形稻田如右下图所示,中间有一条平行四边形水渠通过。算一算,这块稻田的实际种植面积是多少平方米?
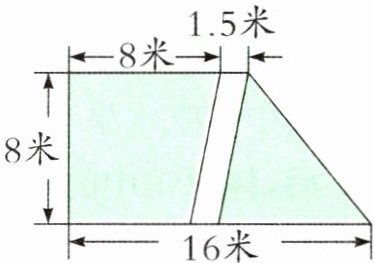

答案:
$(8+1.5+16)× 8÷ 2-1.5× 8=90(\text{平方米})$
6. 实验班原创 几何直观 小明学校即将开展运动会,学校要在每个班召集志愿者。小明在当志愿者的过程中发现操场上有很多指示牌(如右下图),这块指示牌的面积是多少平方分米?
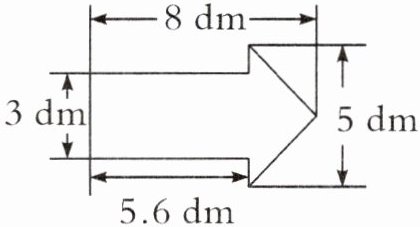

答案:
$5.6× 3+5× (8-5.6)÷ 2=22.8(\text{dm}^2)$
【提示】观察图形,指示牌可以分成一个长方形和一个三角形,利用已知条件求出三角形和长方形的面积,将两个图形面积相加即可。
【提示】观察图形,指示牌可以分成一个长方形和一个三角形,利用已知条件求出三角形和长方形的面积,将两个图形面积相加即可。
7. 阳光社区进行环境美化,准备在一块长 $ 20 \mathrm{m} $、宽 $ 10 \mathrm{m} $ 的长方形空地中间修建一个六边形喷水池(如右下图),涂色部分为草坪。算一算,新建成的喷水池的占地面积是多少平方米?
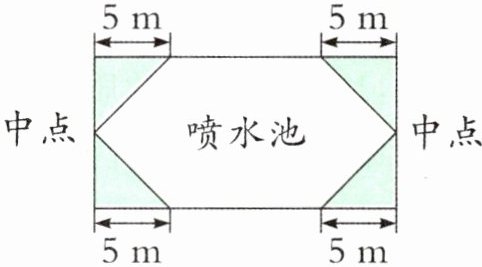

答案:
$20× 10-5× (10÷ 2)÷ 2× 4=150(\text{m}^2)$
【提示】喷水池的面积就是长方形空地的面积减去四个角上的三角形面积,四个三角形完全相同,底都是$5\ \text{m}$,高都是长方形空地宽的一半。
【提示】喷水池的面积就是长方形空地的面积减去四个角上的三角形面积,四个三角形完全相同,底都是$5\ \text{m}$,高都是长方形空地宽的一半。
查看更多完整答案,请扫码查看


