《2025年实验班提优训练五年级数学上册北师大版》

例1 如下图,已知平行四边形的面积是28平方厘米,则涂色部分的面积是多少平方厘米？(单位：厘米)

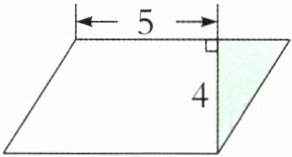
解析
4厘米既是平行四边形的高,也是涂色三角形的高,平行四边形的面积是28平方厘米,底就是$28÷4= 7$(厘米),平行四边形的底减5厘米就是三角形的底$7-5= 2$(厘米),根据三角形面积公式直接求出涂色部分的面积。
答案：$28÷4= 7$(厘米)
$7-5= 2$(厘米)
$2×4÷2= 4$(平方厘米)
答：涂色部分的面积是4平方厘米。
小结
解决本题的关键是利用已知条件求出三角形的底。

答案： 解析：
本题主要考查平行四边形和三角形面积公式的应用，关键在于通过平行四边形的面积和已知的高求出相关底边长度，进而求出涂色部分三角形的面积。
已知平行四边形面积公式为$S = a× h$（$S$表示面积，$a$表示底，$h$表示高），平行四边形面积是$28$平方厘米，高是$4$厘米，那么它的底$a = S÷ h=28÷4 = 7$厘米。
观察图形可知，涂色部分三角形的底是平行四边形的底减去$5$厘米，即$7 - 5 = 2$厘米，而三角形的高与平行四边形的高相等，都是$4$厘米。
根据三角形面积公式$S=\frac{1}{2}× a× h$（$S$表示面积，$a$表示底，$h$表示高），可得涂色部分三角形面积为$\frac{1}{2}×2×4 = 4$平方厘米。
答案：
$28÷4 = 7$（厘米）
$7 - 5 = 2$（厘米）
$2×4÷2 = 4$（平方厘米）
答：涂色部分的面积是$4$平方厘米。

1. 在一个大坝上,路面因长期没有检修而发生凹陷,现如今政府准备出资进行修理。如右下图所示,这是大坝的截面,已知图中三角形的面积为$225m^{2}$,求梯形的面积。

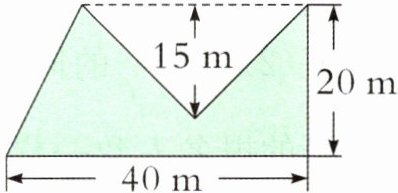
答案： 三角形的底:$225× 2÷ 15=30(\text{m})$
梯形面积:$(30+40)× 20÷ 2=700(\text{m}^2)$
![img alt=视频详讲答案]
【提示】观察图形发现三角形的底就是梯形的上底,根据已知条件先求出三角形的底,再通过梯形面积公式求出梯形的面积。

例2 如下图,三角形甲的面积比三角形乙的面积大6平方厘米,求CE的长度。

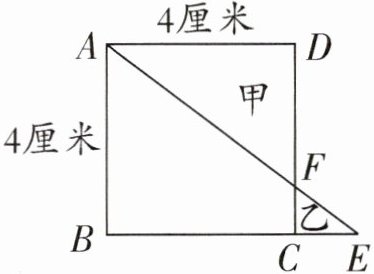
解析
已知三角形甲的面积比三角形乙的面积大6平方厘米,则甲的面积-乙的面积= 6平方厘米,(甲的面积+梯形ABCF的面积)-(乙的面积+梯形ABCF的面积)= 6平方厘米,即正方形ABCD的面积-三角形ABE的面积= 6平方厘米。
答案：三角形ABE的面积：$4×4-6= 10$(平方厘米)
BE的长：$10×2÷4= 5$(厘米)
CE的长：$5-4= 1$(厘米)
答：CE的长度为1厘米。
小结
将待求图形的面积转化成两个其他图形面积的和或差。

答案： 解析：
已知三角形甲的面积比三角形乙的面积大6平方厘米，则$甲的面积 - 乙的面积 = 6平方厘米$。
$(甲的面积 + 梯形ABCF的面积) - (乙的面积 + 梯形ABCF的面积) = 6平方厘米$。
即$正方形ABCD的面积 - 三角形ABE的面积 = 6平方厘米$。
正方形$ABCD$的边长为$4$厘米，所以面积为$4× 4 = 16$（平方厘米）。
设$BE$的长度为$x$厘米，则三角形$ABE$的面积为$\frac{1}{2} × 4 × x = 2x$（平方厘米）。
根据$正方形ABCD的面积 - 三角形ABE的面积 = 6平方厘米$，可得：
$16 - 2x = 6$，
$2x = 10$，
$x = 5$。
所以$BE$的长度为$5$厘米。
因为$BC = 4$厘米，所以$CE = BE - BC = 5 - 4 = 1$（厘米）。
答案：
正方形$ABCD$的面积：$4×4 = 16(平方厘米)$。
三角形$ABE$的面积：$16 - 6 = 10(平方厘米)$。
$BE$的长：$10×2÷4 = 5(厘米)$。
$CE$的长：$5 - 4 = 1(厘米)$。
答：$CE$的长度为$1$厘米。

2. 如右下图,四边形ABCD是一个长10厘米、宽6厘米的长方形。若三角形ADE的面积比三角形CEF的面积大10平方厘米,则CF的长是多少厘米？

答案： 三角形ABF的面积:$10× 6-10=50$(平方厘米)
三角形ABF的边BF的长:$50× 2÷ 10=10$(厘米)
CF的长:$10-6=4$(厘米)
【提示】根据“三角形ADE比三角形CEF的面积大10平方厘米”可知,(长方形ABCD的面积一梯形ABCE的面积)-(三角形ABF的面积一梯形ABCE的面积)$=10$平方厘米,即长方形ABCD的面积比三角形ABF的面积大10平方厘米。因此三角形ABF的面积=长方形ABCD的面积-10平方厘米,再根据三角形面积公式求出三角形ABF的边BF的长,$CF=BF-BC$。