《2025年实验班提优训练五年级数学上册北师大版》

8. 光明小区有一块长方形草坪(如右下图)的面积是 $ 70 \mathrm{m}^{2} $,由于人们长期踩踏,出现了一条小路(涂色部分)。已知 $ B C = 2 B F = 10 \mathrm{m} $, $ B E = 4 \mathrm{m} $,求涂色部分的面积。

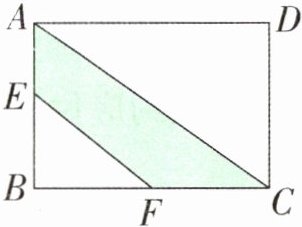
答案： 三角形$BEF$的面积：$(10÷ 2)× 4=10(\text{m}^2)$
三角形$ABC$的面积：$70÷ 2=35(\text{m}^2)$
涂色部分面积：$35-10=25(\text{m}^2)$

9. 手工课上,小明将纸片裁成了如右下图所示的形状,请你计算纸片的面积。(单位：cm)

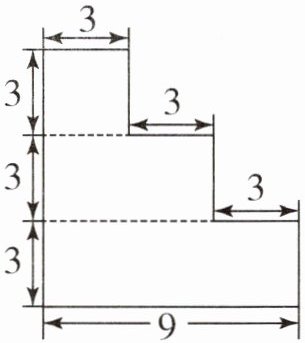
答案： $3× 3+3× (3+3)+3× 9=54(\text{cm}^2)$
【提示】将原图形分成一个边长$3\ \text{cm}$的正方形，一个长$(3+3)\text{cm}$、宽$3\ \text{cm}$的长方形和一个长$9\ \text{cm}$、宽$3\ \text{cm}$的长方形，据此计算即可。

10. 如右下图,两个完全相同的直角梯形重叠在一起,求涂色部分的面积。(单位：cm)

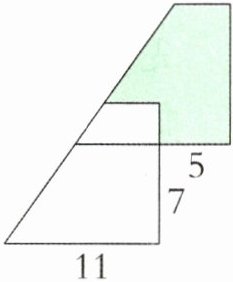
答案： $(11-5+11)× 7÷ 2=59.5(\text{cm}^2)$
【提示】两个直角梯形完全相同，去掉中间重叠的面积，上面梯形中的涂色部分与下面梯形中不重叠部分的面积相同，因此就将涂色部分的面积转化为求上底是$(11-5)\text{cm}$、下底是$11\ \text{cm}$、高是$7\ \text{cm}$的梯形的面积。

11. 如图,莉莉家有个边长是20米的正方形小菜园,为了便于浇水,爷爷在小菜园中修了两条宽为1米的小路。剩余菜地的面积是多少平方米？(单位：米)

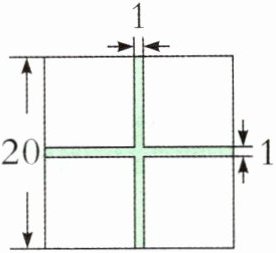
答案： $(20-1)× (20-1)=361(\text{平方米})$
【提示】用平移法，将两条小路平移到正方形小菜园的边上，可以得到一个边长为$(20-1)$米的小正方形菜地，面积是$19× 19=361(\text{平方米})$。

12. 新素养 几何直观 将一张长方形纸片剪一刀,剪成了一个三角形和一个梯形(如下图,单位：cm)。

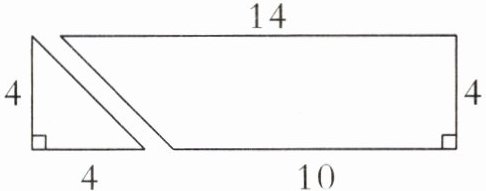
(1)这张长方形纸片的面积是( )平方厘米。
(2)如果在梯形中继续剪,那么最多还可以剪出多少个图中的三角形？(三角形不能拼接)
我用梯形的面积除以三角形的面积,得到最多还可以剪出6个图中的三角形。

你同意小红的说法吗？说出你的理由。如果不同意,那么你认为最多还可以剪出多少个图中的三角形？把你的想法写在下面,或者在图中画一画。

答案：

(1)56
(2)不同意，因为梯形的上、下底分别为$14\ \text{cm}$和$10\ \text{cm}$，都不是4的倍数，也就是说会剩余一部分剪不成图中的三角形。因此，不能直接用梯形的面积除以三角形的面积来求三角形的个数。画图如下：

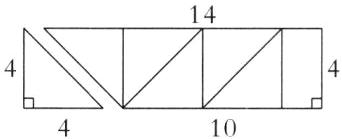
我认为最多还可以剪出5个图中的三角形。