搜索
1. 图形的基本变换方式有(
旋转
)、(平移
)、(轴对称
)。
答案：
旋转 平移 轴对称
2. (
旋转中心
)、(旋转方向
)、(旋转角度
)是旋转变换的三个基本要素。
答案：
旋转中心、旋转方向、旋转角度
3. 看图填一填。
(1) 图①绕点A按(
(2) 图②绕点A按(
(3) 图③绕点A按顺时针方向旋转(
(4) 图④绕点A按顺时针方向旋转(
(1) 图①绕点A按(
逆时针
)方向旋转$90^{\circ }$得到图②。(2) 图②绕点A按(
逆时针
)方向旋转$90^{\circ }$得到图③。(3) 图③绕点A按顺时针方向旋转(
180
)°得到图①。(4) 图④绕点A按顺时针方向旋转(
90
)°得到图③。
答案：
(1)逆时针
(2)逆时针
(3)180
(4)90
(1)逆时针
(2)逆时针
(3)180
(4)90
4. (1) 图形②是由图形①先向
(2) 图形③是由图形②绕点
右
平移3
格,再向下
平移2
格得到的。(或先向下
平移2
格,再向右
平移3
格得到的。)(2) 图形③是由图形②绕点
$C_{1}$
按顺
时针方向旋转90
°得到的。
答案：
(1)右 3 下 2(或下 2 右 3)
(2)$C_{1}$ 顺 90
(1)右 3 下 2(或下 2 右 3)
(2)$C_{1}$ 顺 90
5. 从$7:20到7:45$,分针旋转了(
150
)°。
答案：
解：从7:20到7:45，经过的时间为45 - 20 = 25分钟。
分针60分钟旋转360°，则每分钟旋转360°÷60 = 6°。
25分钟旋转的度数为25×6° = 150°。
150
分针60分钟旋转360°，则每分钟旋转360°÷60 = 6°。
25分钟旋转的度数为25×6° = 150°。
150
6. 如图,三角形ABC绕点C按顺时针方向旋转$120^{\circ }后得到三角形A'B'C$,则点A的对应点是(
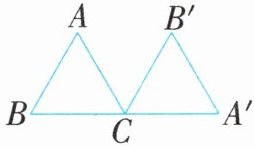
$A'$
),线段AB的对应线段是($A'B'$
),$∠B$的对应角是($∠B'$
),$∠BCB'$的度数是(120
)°。
答案：
点A的对应点是$A'$，线段AB的对应线段是$A'B'$，$∠B$的对应角是$∠B'$，$∠BCB'$的度数是$120$°。
二、明辨是非。
1. 图形的平移、旋转不会改变图形的大小。 (
2.
按顺时针方向旋转$90^{\circ }$后得到的图形是
。 (
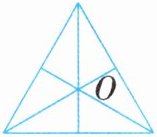
3. 如图,将等边三角形绕点O旋转$120^{\circ }$后与原来的图形重合。 (
1. 图形的平移、旋转不会改变图形的大小。 (
√
)2.
按顺时针方向旋转$90^{\circ }$后得到的图形是。 (×
)3. 如图,将等边三角形绕点O旋转$120^{\circ }$后与原来的图形重合。 (
√
)
答案：
1.√
2.×
3.√
2.×
3.√
1. 下面的图形中,绕点O按顺时针方向旋转$90^{\circ }$后与原图形重合的是(
D
)。
答案：
D
2. 下面的四幅图中,以点A为旋转中心的是(
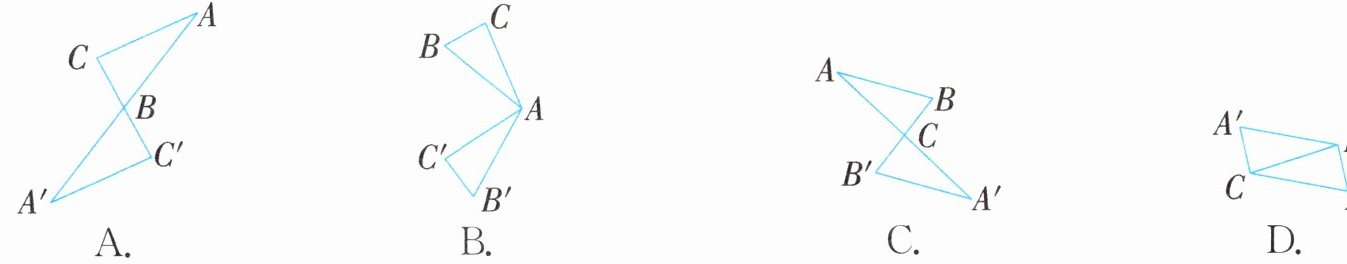
B
)。
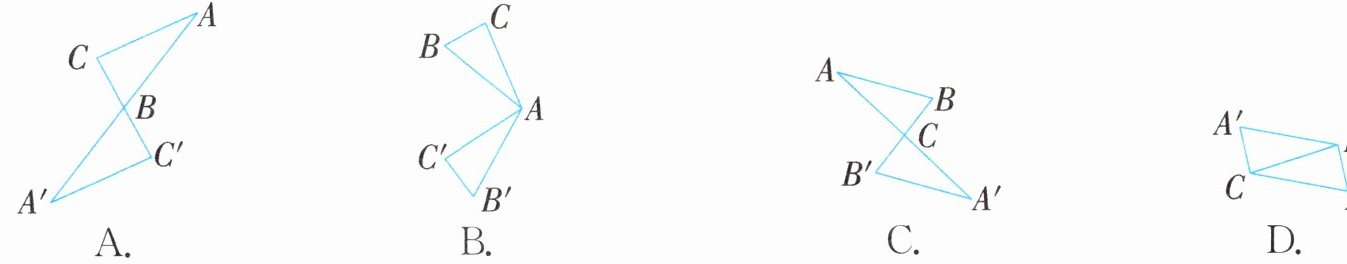
答案：
B
查看更多完整答案，请扫码查看
