例1 甲、乙两车同时从A,B两地相向开出,甲车每小时行56千米,乙车每小时行48千米,两车在距中点32千米处相遇。求A,B两地之间的距离。
点拨:由于甲车速度快,乙车速度慢,甲、乙两车在距中点32千米处相遇,应该是在甲车超过中点,而乙车未到中点的一侧,则甲车比乙车多行了32×2= 64(千米),甲车每小时比乙车多行56-48= 8(千米),据此可以求出相遇时间,进而根据“速度和×时间= 路程”求出A,B两地之间的距离。
解答:
点拨:由于甲车速度快,乙车速度慢,甲、乙两车在距中点32千米处相遇,应该是在甲车超过中点,而乙车未到中点的一侧,则甲车比乙车多行了32×2= 64(千米),甲车每小时比乙车多行56-48= 8(千米),据此可以求出相遇时间,进而根据“速度和×时间= 路程”求出A,B两地之间的距离。
解答:
答案:
解:
32×2=64(千米)
64÷(56-48)=8(时)
(56+48)×8=832(千米)
答:A,B两地之间的距离为832千米。
32×2=64(千米)
64÷(56-48)=8(时)
(56+48)×8=832(千米)
答:A,B两地之间的距离为832千米。
例2 小新每分钟走40米,小伟每分钟走20米,小新家和小伟家相距80米,且小新家离学校更远。两人同时从家中出发去学校,同向而行。小新用4分钟能追上小伟吗?(此时未到学校)
点拨:此题为追及问题,路程差已知,每分钟走的路程差为40-20= 20(米),可根据“追及时间= 路程差÷速度差”,先求出小新追上小伟所用的时间,进而与4分钟相比较即可。此题也可借助线段图来分析两人出发4分钟后出现的情况。(如下图)
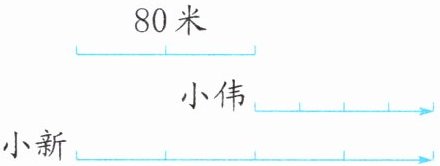
由图可知,两人出发4分钟后相遇,即小新正好追上小伟。
解答:
点拨:此题为追及问题,路程差已知,每分钟走的路程差为40-20= 20(米),可根据“追及时间= 路程差÷速度差”,先求出小新追上小伟所用的时间,进而与4分钟相比较即可。此题也可借助线段图来分析两人出发4分钟后出现的情况。(如下图)

由图可知,两人出发4分钟后相遇,即小新正好追上小伟。
解答:
解:追及时间 = 路程差 ÷ 速度差
$80÷(40-20)=4$(分钟)
$4=4$
答:小新用4分钟能追上小伟。
$80÷(40-20)=4$(分钟)
$4=4$
答:小新用4分钟能追上小伟。
答案:
解:追及时间 = 路程差 ÷ 速度差
$80÷(40-20)=4$(分钟)
$4=4$
答:小新用4分钟能追上小伟。
$80÷(40-20)=4$(分钟)
$4=4$
答:小新用4分钟能追上小伟。
查看更多完整答案,请扫码查看


