3. 如图,甲、乙两条彩带都被遮住了一部分。这两条彩带的总长度相比,(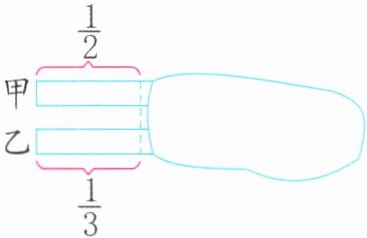
A.甲比乙长
B.乙比甲长
C.一样长
D.无法确定
B
)。
A.甲比乙长
B.乙比甲长
C.一样长
D.无法确定
答案:
B 解析:两条彩带露出的部分一样长,甲露出$\frac{1}{2}$,说明全长是露出部分的2倍;乙露出$\frac{1}{3}$,说明全长是露出部分的3倍。所以乙比甲长。
4. 将一张正方形纸连续对折四次后,得到的图形的面积是原来的(
A.$\frac {1}{2}$
B.$\frac {1}{4}$
C.$\frac {1}{8}$
D.$\frac {1}{16}$
D
)。A.$\frac {1}{2}$
B.$\frac {1}{4}$
C.$\frac {1}{8}$
D.$\frac {1}{16}$
答案:
设原正方形纸的面积为1。
第一次对折后,面积变为原来的$\frac{1}{2}$,即$1×\frac{1}{2}=\frac{1}{2}$;
第二次对折后,面积变为第一次对折后面积的$\frac{1}{2}$,即$\frac{1}{2}×\frac{1}{2}=\frac{1}{4}$;
第三次对折后,面积变为第二次对折后面积的$\frac{1}{2}$,即$\frac{1}{4}×\frac{1}{2}=\frac{1}{8}$;
第四次对折后,面积变为第三次对折后面积的$\frac{1}{2}$,即$\frac{1}{8}×\frac{1}{2}=\frac{1}{16}$。
D
第一次对折后,面积变为原来的$\frac{1}{2}$,即$1×\frac{1}{2}=\frac{1}{2}$;
第二次对折后,面积变为第一次对折后面积的$\frac{1}{2}$,即$\frac{1}{2}×\frac{1}{2}=\frac{1}{4}$;
第三次对折后,面积变为第二次对折后面积的$\frac{1}{2}$,即$\frac{1}{4}×\frac{1}{2}=\frac{1}{8}$;
第四次对折后,面积变为第三次对折后面积的$\frac{1}{2}$,即$\frac{1}{8}×\frac{1}{2}=\frac{1}{16}$。
D
1. 先通分,再比较每组中两个分数的大小。
$\frac {11}{15}和\frac {7}{10}$ $\frac {5}{6}和\frac {31}{36}$ $\frac {5}{8}和\frac {3}{7}$ $\frac {9}{20}和\frac {1}{3}$
$\frac {11}{15}和\frac {7}{10}$ $\frac {5}{6}和\frac {31}{36}$ $\frac {5}{8}和\frac {3}{7}$ $\frac {9}{20}和\frac {1}{3}$
答案:
$\frac{11}{15}=\frac{22}{30}$,$\frac{7}{10}=\frac{21}{30}$,因为$\frac{22}{30}>\frac{21}{30}$,所以$\frac{11}{15}>\frac{7}{10}$;
$\frac{5}{6}=\frac{30}{36}$,因为$\frac{30}{36}<\frac{31}{36}$,所以$\frac{5}{6}<\frac{31}{36}$;
$\frac{5}{8}=\frac{35}{56}$,$\frac{3}{7}=\frac{24}{56}$,因为$\frac{35}{56}>\frac{24}{56}$,所以$\frac{5}{8}>\frac{3}{7}$;
$\frac{9}{20}=\frac{27}{60}$,$\frac{1}{3}=\frac{20}{60}$,因为$\frac{27}{60}>\frac{20}{60}$,所以$\frac{9}{20}>\frac{1}{3}$。
$\frac{5}{6}=\frac{30}{36}$,因为$\frac{30}{36}<\frac{31}{36}$,所以$\frac{5}{6}<\frac{31}{36}$;
$\frac{5}{8}=\frac{35}{56}$,$\frac{3}{7}=\frac{24}{56}$,因为$\frac{35}{56}>\frac{24}{56}$,所以$\frac{5}{8}>\frac{3}{7}$;
$\frac{9}{20}=\frac{27}{60}$,$\frac{1}{3}=\frac{20}{60}$,因为$\frac{27}{60}>\frac{20}{60}$,所以$\frac{9}{20}>\frac{1}{3}$。
2. 把下面各数化成最简分数。
$\frac {16}{36}=$
$\frac {16}{36}=$
$\frac{4}{9}$
$\frac {100}{60}=$$\frac{5}{3}$
$1\frac {22}{66}=$$1\frac{1}{3}$
$\frac {34}{51}=$$\frac{2}{3}$
答案:
$\frac{16}{36}=\frac{16÷4}{36÷4}=\frac{4}{9}$
$\frac{100}{60}=\frac{100÷20}{60÷20}=\frac{5}{3}$
$1\frac{22}{66}=1\frac{22÷22}{66÷22}=1\frac{1}{3}=\frac{4}{3}$
$\frac{34}{51}=\frac{34÷17}{51÷17}=\frac{2}{3}$
$\frac{100}{60}=\frac{100÷20}{60÷20}=\frac{5}{3}$
$1\frac{22}{66}=1\frac{22÷22}{66÷22}=1\frac{1}{3}=\frac{4}{3}$
$\frac{34}{51}=\frac{34÷17}{51÷17}=\frac{2}{3}$
五、正确操作。
在下面各图形中涂色表示出$\frac {2}{5}$吨。
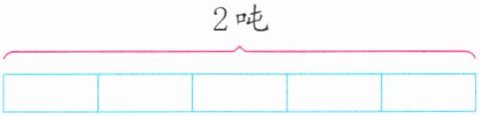
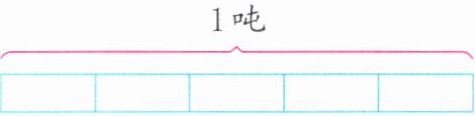
在下面各图形中涂色表示出$\frac {2}{5}$吨。


答案:




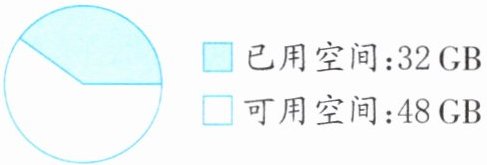
1. 下图反映的是一个磁盘的存储情况。已用空间占磁盘总容量的几分之几?

答案:
解:磁盘总容量为 $32 + 48 = 80$(GB)
已用空间占比为 $32 ÷ 80 = \frac{32}{80} = \frac{2}{5}$
答:已用空间占磁盘总容量的$\frac{2}{5}$
已用空间占比为 $32 ÷ 80 = \frac{32}{80} = \frac{2}{5}$
答:已用空间占磁盘总容量的$\frac{2}{5}$
2. 有两根铁丝,一根长36分米,另一根长24分米,把它们全部截成长度相等的小段,没有剩余,每段最长是多少分米? 一共可以截成多少段?
答案:
解:36和24的最大公因数是12。
36÷12 + 24÷12 = 3 + 2 = 5(段)
每段最长是12分米,一共可以截成5段。
36÷12 + 24÷12 = 3 + 2 = 5(段)
每段最长是12分米,一共可以截成5段。
3. 某公共汽车站是1路车和5路车的起点站,早上$6:30$同时发出第一辆车后,1路车每15分钟发一辆,5路车每12分钟发一辆,从早上$6:30$开始,至少再过多少分钟又同时发车? 这时是几时几分?
解:15和12的最小公倍数是60。
至少再过60分钟又同时发车。
6时30分+60分=7时30分。
答:至少再过60分钟又同时发车,这时是7时30分。
解:15和12的最小公倍数是60。
至少再过60分钟又同时发车。
6时30分+60分=7时30分。
答:至少再过60分钟又同时发车,这时是7时30分。
答案:
解:15和12的最小公倍数是60。
至少再过60分钟又同时发车。
6时30分+60分=7时30分。
答:至少再过60分钟又同时发车,这时是7时30分。
至少再过60分钟又同时发车。
6时30分+60分=7时30分。
答:至少再过60分钟又同时发车,这时是7时30分。
查看更多完整答案,请扫码查看


