2. 把一个长30厘米、宽21厘米、高18厘米的长方体木块切成大小相等的小正方体木块,且没有剩余。小正方体木块的棱长最大是几厘米? 能切成多少个? (4分)
答案:
解:30、21和18的最大公因数是3。
小正方体木块的棱长最大是3厘米。
$(30÷3)×(21÷3)×(18÷3)=10×7×6=420$(个)
答:小正方体木块的棱长最大是3厘米,能切成420个。
小正方体木块的棱长最大是3厘米。
$(30÷3)×(21÷3)×(18÷3)=10×7×6=420$(个)
答:小正方体木块的棱长最大是3厘米,能切成420个。
3. 有两个形状、大小完全相同的物体(如图),现用包装纸将它们一起包装起来,至少需要多少平方厘米的包装纸? (损耗忽略不计)(4分)


答案:
解:将两个物体叠放,使最大面重合,此时新长方体的长为8cm,宽为7cm,高为$1 + 1 = 2$cm。
表面积为$[8×7 + 7×2 + 8×2]×2$
$=(56 + 14 + 16)×2$
$=86×2$
$=172(cm^{2})$
答:至少需要172平方厘米的包装纸。
表面积为$[8×7 + 7×2 + 8×2]×2$
$=(56 + 14 + 16)×2$
$=86×2$
$=172(cm^{2})$
答:至少需要172平方厘米的包装纸。
4. 一个长方体,高增加4cm后变成了棱长是10cm的正方体,表面积和体积各增加了多少? (4分)
答案:
解:表面积增加:$10×4×4 = 160(cm^{2})$
体积增加:$10×10×4 = 400(cm^{3})$
答:表面积增加了$160cm^{2}$,体积增加了$400cm^{3}$。
体积增加:$10×10×4 = 400(cm^{3})$
答:表面积增加了$160cm^{2}$,体积增加了$400cm^{3}$。
5. 如图,一个长方体容器,从里面量,长和宽都是3dm。先向空的容器中倒入11.7L水,再把一个石块完全浸入水中(水未溢出),这时容器内的水深是15cm。这个石块的体积是多少立方分米? (4分)
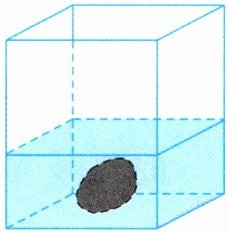

答案:
$11.7L=11.7dm^{3}$
$15cm=1.5dm$
$3×3×1.5 - 11.7$
$=9×1.5 - 11.7$
$=13.5 - 11.7$
$=1.8(dm^{3})$
答:这个石块的体积是$1.8$立方分米。
$15cm=1.5dm$
$3×3×1.5 - 11.7$
$=9×1.5 - 11.7$
$=13.5 - 11.7$
$=1.8(dm^{3})$
答:这个石块的体积是$1.8$立方分米。
6. 李老师与五(1)班的同学们讨论这样一个问题:如果假期中有急事需要打电话(每打一通电话需要1分钟)通知大家,那么李老师至少要花几分钟才能尽快通知全班的45名同学? (4分)
答案:
解:1分钟:1人(老师通知1名学生)
2分钟:1+2=3人(老师和1名学生各通知1人,共新增2人)
3分钟:3+4=7人(新增4人)
4分钟:7+8=15人(新增8人)
5分钟:15+16=31人(新增16人)
6分钟:31+32=63人(新增32人)
63>45
答:至少要花6分钟。
2分钟:1+2=3人(老师和1名学生各通知1人,共新增2人)
3分钟:3+4=7人(新增4人)
4分钟:7+8=15人(新增8人)
5分钟:15+16=31人(新增16人)
6分钟:31+32=63人(新增32人)
63>45
答:至少要花6分钟。
7. 在$\underbrace{222…222}_{2023个2}□$这个数中,$□$里最小填几,这个数就是3的倍数? (5分)
解:2023个2的和为$2023×2 = 4046$,$4046÷3 = 1348\cdots\cdots2$,因为一个数是3的倍数,其各位数字之和必须是3的倍数,所以$3 - 2 = 1$,故$□$里最小填1。
答:$□$里最小填1。
答:$□$里最小填1。
答案:
解:2023个2的和为$2023×2 = 4046$,$4046÷3 = 1348\cdots\cdots2$,因为一个数是3的倍数,其各位数字之和必须是3的倍数,所以$3 - 2 = 1$,故$□$里最小填1。
答:$□$里最小填1。
答:$□$里最小填1。
查看更多完整答案,请扫码查看


