1. 如果$a÷b= 2$(a,b 都是非 0 自然数),那么 a 是 b 的(
倍数
),b 是 a 的(因数
)。
答案:
倍数 因数
2. 20 的因数有(
1,2,4,5,10,20
);整数中,是 2 的倍数的数叫作(偶数
)。
答案:
1,2,4,5,10,20 偶数
3. 在 14,17,22,45,100,87,37,96,29 这些数中,3 的倍数有
45,87,96
,2 的倍数有14,22,100,96
,5 的倍数有45,100
,质数有17,37,29
,合数有14,22,45,100,87,96
,奇数有17,45,87,37,29
。
答案:
3 的倍数有(45,87,96),2 的倍数有(14,22,100,96),5 的倍数有(45,100),质数有(17,37,29),合数有(14,22,45,100,87,96),奇数有(17,45,87,37,29)。
4. 在自然数中,最小的质数是(
2
),最小的合数是(4
),(1
)是最小的奇数。
答案:
2 4 1
5. 在括号里填上适当的质数。
$14= ($
$14= ($
2
$)+ ($5
$)+ ($7
$)$ $30= ($2
$)× ($3
$)× ($5
$)$
答案:
14 =
(2) +
(5) +
(7)
30 =
(2) ×
(3) ×
(5)
(2) +
(5) +
(7)
30 =
(2) ×
(3) ×
(5)
6. 一个数既是 2 的倍数,又是 5 的倍数。若这个数是两位数,则最大是
90
;若这个数是三位数,则最小是100
。
答案:
既是2的倍数又是5的倍数的数的特征是个位上是0。
两位数中最大的个位是0的数是90;
三位数中最小的个位是0的数是100。
90;100
两位数中最大的个位是0的数是90;
三位数中最小的个位是0的数是100。
90;100
7. 67 至少减去
1
后是 3 的倍数,至少加上3
后有因数 5。
答案:
67各个数位上数字之和为6+7=13,13除以3商4余1,所以至少减去1后是3的倍数;67除以5商13余2,5-2=3,所以至少加上3后有因数5。
1 3
1 3
8. 用若干个同样大小的正方体搭一个物体,从不同方向看到的图形
如右图所示,则这个物体是由(

如右图所示,则这个物体是由(
5
)个同样大小的正方体搭成的。
答案:
解:根据从上面看到的图形,底层有3个正方体(前排2个,后排1个)。
从前面看,前排最高2层,后排最高1层;从右面看,右侧最高2层,左侧最高1层。
综合判断,前排右侧正方体上有1个正方体,后排左侧正方体上有1个正方体。
总个数:3 + 1 + 1 = 5。
答案:5
从前面看,前排最高2层,后排最高1层;从右面看,右侧最高2层,左侧最高1层。
综合判断,前排右侧正方体上有1个正方体,后排左侧正方体上有1个正方体。
总个数:3 + 1 + 1 = 5。
答案:5
9. 三个连续偶数的和是 60,其中最小的偶数是(
18
),最大的偶数是(22
)。
答案:
解:设最小的偶数为$x$,则另两个连续偶数分别为$x + 2$,$x + 4$。
$x + (x + 2) + (x + 4) = 60$
$3x + 6 = 60$
$3x = 54$
$x = 18$
最大的偶数为$x + 4 = 18 + 4 = 22$
18;22
$x + (x + 2) + (x + 4) = 60$
$3x + 6 = 60$
$3x = 54$
$x = 18$
最大的偶数为$x + 4 = 18 + 4 = 22$
18;22
10. 若一个质数分别加上 2,8,14,26 后,得到的和都是质数,则这个质数是(
3
)或(5
)。
答案:
解:
1. 当这个质数为3时:
3+2=5(质数),3+8=11(质数),3+14=17(质数),3+26=29(质数),均符合条件。
2. 当这个质数为5时:
5+2=7(质数),5+8=13(质数),5+14=19(质数),5+26=31(质数),均符合条件。
3 5
1. 当这个质数为3时:
3+2=5(质数),3+8=11(质数),3+14=17(质数),3+26=29(质数),均符合条件。
2. 当这个质数为5时:
5+2=7(质数),5+8=13(质数),5+14=19(质数),5+26=31(质数),均符合条件。
3 5
二、明辨是非。
1. 一个数的最小倍数是它本身,没有最大因数。 (
2. 若一个物体从前面看到的图形是,则这个物体一定是由 2 个小正方体搭成的。 (
3. 正方形的边长是质数,它的面积一定是合数。 (
4. 三个连续非 0 自然数中一定有一个是 3 的倍数。 (
1. 一个数的最小倍数是它本身,没有最大因数。 (
×
)2. 若一个物体从前面看到的图形是,则这个物体一定是由 2 个小正方体搭成的。 (
×
)3. 正方形的边长是质数,它的面积一定是合数。 (
√
)4. 三个连续非 0 自然数中一定有一个是 3 的倍数。 (
√
)
答案:
1. ×
2. ×
3. √
4. √
2. ×
3. √
4. √
1. 下面各数中,因数个数最多的是(
A.18
B.48
C.60
D.63
C
)。A.18
B.48
C.60
D.63
答案:
18的因数:1、2、3、6、9、18,共6个;
48的因数:1、2、3、4、6、8、12、16、24、48,共10个;
60的因数:1、2、3、4、5、6、10、12、15、20、30、60,共12个;
63的因数:1、3、7、9、21、63,共6个。
因数个数最多的是60。
答案:C
48的因数:1、2、3、4、6、8、12、16、24、48,共10个;
60的因数:1、2、3、4、5、6、10、12、15、20、30、60,共12个;
63的因数:1、3、7、9、21、63,共6个。
因数个数最多的是60。
答案:C
2. 甲是乙的倍数,丙是乙的因数,那么甲是丙的(
A.倍数
B.因数
C.既不是因数也不是倍数
D.无法确定
A
)。A.倍数
B.因数
C.既不是因数也不是倍数
D.无法确定
答案:
解:设乙为$a$($a$为正整数)。
因为甲是乙的倍数,所以甲可表示为$k× a$($k$为正整数)。
因为丙是乙的因数,所以乙可表示为$m×$丙($m$为正整数),即丙$=\frac{a}{m}$。
则甲$=k× a = k× m×$丙,所以甲是丙的倍数。
答案:A
因为甲是乙的倍数,所以甲可表示为$k× a$($k$为正整数)。
因为丙是乙的因数,所以乙可表示为$m×$丙($m$为正整数),即丙$=\frac{a}{m}$。
则甲$=k× a = k× m×$丙,所以甲是丙的倍数。
答案:A
3. 用同样大小的正方体摆一个物体,从前面看到的是, 从上面看到的是,
从上面看到的是, 从左面看到的是(
从左面看到的是(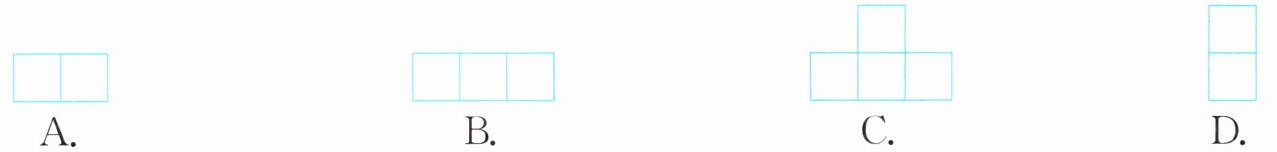
 从上面看到的是,
从上面看到的是, 从左面看到的是(
从左面看到的是(A
)。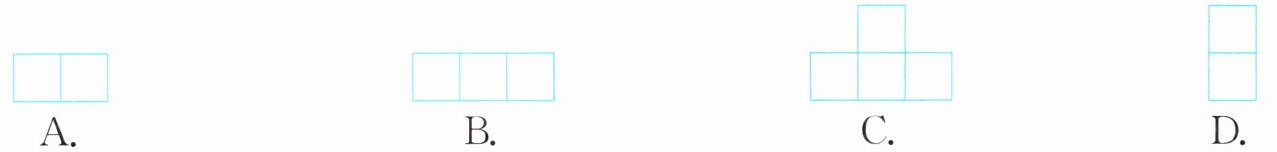
答案:
解:根据从前面和上面看到的图形,可确定该物体底层有3个正方体(前排2个,后排1个靠右),第二层有1个正方体(后排靠右)。从左面看,底层有2个正方体(前后各1个),第二层有1个正方体(后排),所以从左面看到的图形为选项A。
答案:A
答案:A
查看更多完整答案,请扫码查看


