《2025年暑期升级训练五年级数学人教版浙江教育出版社》

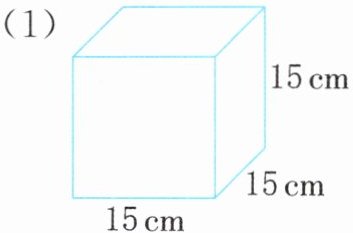
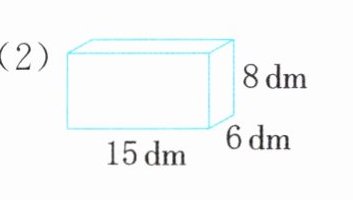
1. 计算下面各图形的体积。

答案：
(1)$15×15×15=3375(cm^{3})$
(2)$15×6×8=720(dm^{3})$

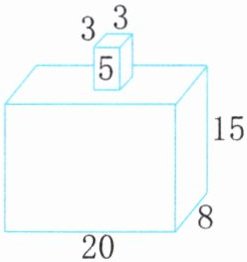
2. 计算下面图形的表面积和体积。(单位:cm)

答案： 表面积：$(20×8 + 20×15 + 15×8 + 5×3 + 5×3)×2$
$=(160 + 300 + 120 + 15 + 15)×2$
$=(580 + 30)×2$
$=610×2$
$=1220(cm^{2})$
体积：$20×8×15 + 5×3×3$
$=2400 + 45$
$=2445(cm^{3})$
答：图形的表面积是$1220cm^{2}$，体积是$2445cm^{3}$。

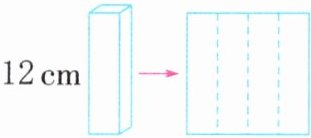
1. 如图,一个底面是正方形的长方体纸盒,将它的侧面展开后正好得到一个正方形,纸盒的高是12 cm。这个纸盒的表面积是多少平方厘米?

答案： 解：因为长方体侧面展开是正方形，所以底面周长等于高，即底面周长为12cm。
底面边长：$12÷4 = 3(cm)$
表面积：$3×3×2 + 3×12×4$
$=18 + 144$
$=162(cm^{2})$
答：这个纸盒的表面积是162平方厘米。

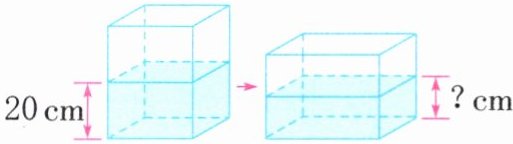
2. 一个封闭的长方体容器(如图),它的长、宽、高分别是 30 cm,30 cm,40 cm,里面装着水,可可不小心把容器碰倒了。现在水的高度是多少厘米?(容器的厚度忽略不计)

答案： 解：水的体积为 $30 × 30 × 20 = 18000 \, \text{cm}^3$。
碰倒后容器的底面积为 $40 × 30 = 1200 \, \text{cm}^2$。
现在水的高度为 $18000 ÷ 1200 = 15 \, \text{cm}$。
答：现在水的高度是15厘米。

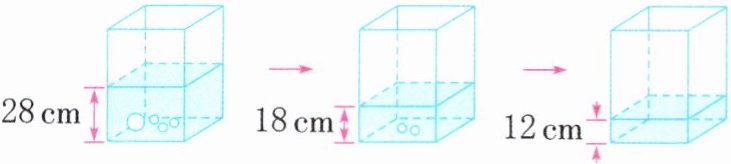
3. 如图,透明玻璃容器的底面积是$80cm^{2}$,观察图中水面高度的变化,求大圆球的体积。

解：
1. 计算2个小圆球的体积：
容器底面积为 $80 \, \text{cm}^2$，第二次水面下降高度 $18 - 12 = 6 \, \text{cm}$，
则2个小圆球体积为 $80 × 6 = 480 \, \text{cm}^3$，
1个小圆球体积为 $480 ÷ 2 = 240 \, \text{cm}^3$。
2. 计算大圆球体积：
第一次水面下降高度 $28 - 18 = 10 \, \text{cm}$，
1大1小两球总体积为 $80 × 10 = 800 \, \text{cm}^3$，
大圆球体积为 $800 - 240 = 560 \, \text{cm}^3$。
答：大圆球的体积是 $560 \, \text{cm}^3$。

答案： 解：
1. 计算2个小圆球的体积：
容器底面积为 $80 \, \text{cm}^2$，第二次水面下降高度 $18 - 12 = 6 \, \text{cm}$，
则2个小圆球体积为 $80 × 6 = 480 \, \text{cm}^3$，
1个小圆球体积为 $480 ÷ 2 = 240 \, \text{cm}^3$。
2. 计算大圆球体积：
第一次水面下降高度 $28 - 18 = 10 \, \text{cm}$，
1大1小两球总体积为 $80 × 10 = 800 \, \text{cm}^3$，
大圆球体积为 $800 - 240 = 560 \, \text{cm}^3$。
答：大圆球的体积是 $560 \, \text{cm}^3$。