1. 下面的物体中,(
A.一个粉笔盒
B.一个集装箱
C.一块橡皮
D.一块巧克力
A
)的体积接近1$dm^{3}$。A.一个粉笔盒
B.一个集装箱
C.一块橡皮
D.一块巧克力
答案:
解析:本题可根据对体积单位$1dm^{3}$的认识,结合生活实际来判断各选项物体的体积大小。
体积单位$1dm^{3}$可以想象成一个棱长为$1dm$(即$10cm$)的正方体的体积大小。
选项A:一个粉笔盒的长、宽、高大约都在$10cm$左右,其体积接近$1dm^{3}$,该选项符合题意。
选项B:一个集装箱的体积非常大,远远大于$1dm^{3}$,该选项不符合题意。
选项C:一块橡皮的体积较小,通常远小于$1dm^{3}$,该选项不符合题意。
选项D:一块巧克力的体积也比较小,一般小于$1dm^{3}$,该选项不符合题意。
答案:A。
体积单位$1dm^{3}$可以想象成一个棱长为$1dm$(即$10cm$)的正方体的体积大小。
选项A:一个粉笔盒的长、宽、高大约都在$10cm$左右,其体积接近$1dm^{3}$,该选项符合题意。
选项B:一个集装箱的体积非常大,远远大于$1dm^{3}$,该选项不符合题意。
选项C:一块橡皮的体积较小,通常远小于$1dm^{3}$,该选项不符合题意。
选项D:一块巧克力的体积也比较小,一般小于$1dm^{3}$,该选项不符合题意。
答案:A。
2. 几个质数相乘的积一定是(
A.质数
B.合数
C.偶数
D.无法确定
B
)。A.质数
B.合数
C.偶数
D.无法确定
答案:
解析:本题可根据质数与合数的定义来判断几个质数相乘的积的性质。
质数是指在大于$1$的自然数中,除了$1$和它本身以外不再有其他因数的自然数。
合数是指自然数中除了能被$1$和本身整除外,还能被其他数($0$除外)整除的数。
几个质数相乘的积,除了$1$和它本身以外,这几个质数也是它的因数,所以几个质数相乘的积一定是合数。
例如$2×3 = 6$,$6$的因数有$1$、$2$、$3$、$6$,除了$1$和$6$本身外,还有$2$和$3$这两个因数,所以$6$是合数。
答案:B。
质数是指在大于$1$的自然数中,除了$1$和它本身以外不再有其他因数的自然数。
合数是指自然数中除了能被$1$和本身整除外,还能被其他数($0$除外)整除的数。
几个质数相乘的积,除了$1$和它本身以外,这几个质数也是它的因数,所以几个质数相乘的积一定是合数。
例如$2×3 = 6$,$6$的因数有$1$、$2$、$3$、$6$,除了$1$和$6$本身外,还有$2$和$3$这两个因数,所以$6$是合数。
答案:B。
3. 把两个棱长是2dm的正方体拼成一个长方体,这个长方体的表面积是(
A.32
B.40
C.48
D.60
B
)$dm^{2}$。A.32
B.40
C.48
D.60
答案:
解析:
本题考查了长方体的表面积计算知识点。
两个正方体拼成长方体后,表面积会减少两个正方形的面积。
每个正方体的棱长是$2dm$,
所以每个面的面积是 $2× 2=4(dm^{2})$ 。
两个正方体总共有 $12$ 个面,
如果单独计算,总面积是 $4× 12=48(dm^{2})$ 。
但拼成长方体时,两个正方体合并去掉了两个面,
所以长方体的表面积应该是 $48-2× 4=40(dm^{2})$ 。
答案:B。
本题考查了长方体的表面积计算知识点。
两个正方体拼成长方体后,表面积会减少两个正方形的面积。
每个正方体的棱长是$2dm$,
所以每个面的面积是 $2× 2=4(dm^{2})$ 。
两个正方体总共有 $12$ 个面,
如果单独计算,总面积是 $4× 12=48(dm^{2})$ 。
但拼成长方体时,两个正方体合并去掉了两个面,
所以长方体的表面积应该是 $48-2× 4=40(dm^{2})$ 。
答案:B。
4. 小明、小华和小芳各做一架相同的航模飞机,小明用了$\frac{3}{4}$小时,小华用了$\frac{5}{6}$小时,小芳用了0.8小时。(
A.小明
B.小华
C.小芳
D.无法确定谁
A
)做得最快。A.小明
B.小华
C.小芳
D.无法确定谁
答案:
解析:本题考查了分数与小数的大小比较以及实际应用。要比较三者谁做得最快,则比较三者所用时间,用时短者做得快。需要将分数$\frac{3}{4}$,$\frac{5}{6}$转化为小数或者将0.8转化为分数,然后进行比较。
$\frac{3}{4}=3÷4=0.75$(小时),
$\frac{5}{6}=5÷6\approx0.833$(小时)(保留三位小数),
比较三者用时:$0.75<0.8<0.833$,
即$\frac{3}{4}<0.8<\frac{5}{6}$,
小明用时最短,所以小明做得最快。
答案:A。
$\frac{3}{4}=3÷4=0.75$(小时),
$\frac{5}{6}=5÷6\approx0.833$(小时)(保留三位小数),
比较三者用时:$0.75<0.8<0.833$,
即$\frac{3}{4}<0.8<\frac{5}{6}$,
小明用时最短,所以小明做得最快。
答案:A。
5. 下面是从三个方向观察一个物体所得到的图形,搭这个物体需要用(
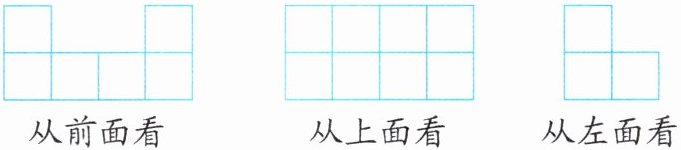
A.9
B.10
C.11
D.12
B
)个同样大小的正方体。
A.9
B.10
C.11
D.12
答案:
解析:本题可根据从不同方向观察到的图形,逐步确定每个位置上正方体的个数,进而计算出搭成这个物体所需正方体的总数。
从上面看:可以确定底层正方体的分布情况,底层有$7$个正方体。
从前面看:能知道这个物体有两层,且第一层(底层)的排列情况与从上面看到的一致,第二层有$3$个正方体。
从左面看:同样能确定有两层,且结合前面和上面的视图,可进一步确认第二层有$3$个正方体。
综合以上三个方向的视图,搭成这个物体所需正方体的总数为底层$7$个加上第二层$3$个,即$7 + 3= 10$(个)。
答案:B。
从上面看:可以确定底层正方体的分布情况,底层有$7$个正方体。
从前面看:能知道这个物体有两层,且第一层(底层)的排列情况与从上面看到的一致,第二层有$3$个正方体。
从左面看:同样能确定有两层,且结合前面和上面的视图,可进一步确认第二层有$3$个正方体。
综合以上三个方向的视图,搭成这个物体所需正方体的总数为底层$7$个加上第二层$3$个,即$7 + 3= 10$(个)。
答案:B。
6. 1杯纯牛奶,芳芳喝了半杯后,兑满水,喝完了,芳芳一共喝了(
A.$\frac{3}{4}$
B.1
C.$\frac{3}{2}$
D.$\frac{1}{4}$
B
)杯纯牛奶。A.$\frac{3}{4}$
B.1
C.$\frac{3}{2}$
D.$\frac{1}{4}$
答案:
解析:本题主要考查分数的计算。
芳芳最开始有一杯纯牛奶。
她先喝了半杯,那么剩下半杯纯牛奶。
然后她兑满了水,但此时纯牛奶的部分仍然是那剩下的半杯。
之后,芳芳又喝完了整杯混合液体(半杯纯牛奶和半杯水)。
所以,芳芳总共喝的纯牛奶是:
最开始喝的半杯 + 后来喝的半杯 = 1杯。
答案:B。
芳芳最开始有一杯纯牛奶。
她先喝了半杯,那么剩下半杯纯牛奶。
然后她兑满了水,但此时纯牛奶的部分仍然是那剩下的半杯。
之后,芳芳又喝完了整杯混合液体(半杯纯牛奶和半杯水)。
所以,芳芳总共喝的纯牛奶是:
最开始喝的半杯 + 后来喝的半杯 = 1杯。
答案:B。
1. 直接写出得数。(8分)
$\frac{5}{7}+\frac{3}{7}=$
$\frac{9}{8}-\frac{1}{8}=$
$\frac{5}{7}+\frac{3}{7}=$
$\frac{8}{7}$
$\frac{19}{25}-\frac{14}{25}=$$\frac{1}{5}$
$\frac{5}{9}+\frac{2}{9}=$$\frac{7}{9}$
$1-\frac{8}{17}=$$\frac{9}{17}$
$\frac{9}{8}-\frac{1}{8}=$
1
$\frac{1}{4}+\frac{1}{5}=$$\frac{9}{20}$
$\frac{1}{2}-\frac{1}{3}=$$\frac{1}{6}$
$\frac{5}{6}+\frac{1}{2}=$$\frac{4}{3}$
答案:
$\frac{8}{7}$ $\frac{1}{5}$ $\frac{7}{9}$ $\frac{9}{17}$ 1 $\frac{9}{20}$ $\frac{1}{6}$ $\frac{4}{3}$
2. 计算下面各题,怎样简便就怎样计算。(12分)
$1-(\frac{8}{9}-\frac{1}{2})$
$\frac{11}{16}+\frac{3}{10}+\frac{5}{16}-\frac{1}{10}$
$1-(\frac{8}{9}-\frac{1}{2})$
$\frac{11}{18}$
$\frac{8}{9}-\frac{5}{13}+\frac{1}{9}$$\frac{8}{13}$
$\frac{2}{5}+\frac{4}{11}+\frac{7}{11}+\frac{8}{5}$3
$\frac{11}{16}+\frac{3}{10}+\frac{5}{16}-\frac{1}{10}$
$1\frac{1}{5}$
$\frac{7}{9}+\frac{3}{5}-(\frac{7}{9}-\frac{3}{5})$$\frac{6}{5}$
$12\frac{4}{5}-(8\frac{4}{5}+3\frac{1}{4})$$\frac{3}{4}$
答案:
1. $1-(\frac{8}{9}-\frac{1}{2})$
$=1-(\frac{16}{18}-\frac{9}{18})$
$=1-\frac{7}{18}$
$=\frac{11}{18}$
2. $\frac{8}{9}-\frac{5}{13}+\frac{1}{9}$
$=(\frac{8}{9}+\frac{1}{9})-\frac{5}{13}$
$=1-\frac{5}{13}$
$=\frac{8}{13}$
3. $\frac{2}{5}+\frac{4}{11}+\frac{7}{11}+\frac{8}{5}$
$=(\frac{2}{5}+\frac{8}{5})+(\frac{4}{11}+\frac{7}{11})$
$=2+1$
$=3$
4. $\frac{11}{16}+\frac{3}{10}+\frac{5}{16}-\frac{1}{10}$
$=(\frac{11}{16}+\frac{5}{16})+(\frac{3}{10}-\frac{1}{10})$
$=1+\frac{2}{10}$
$=1+\frac{1}{5}$
$=1\frac{1}{5}$
5. $\frac{7}{9}+\frac{3}{5}-(\frac{7}{9}-\frac{3}{5})$
$=\frac{7}{9}+\frac{3}{5}-\frac{7}{9}+\frac{3}{5}$
$=(\frac{7}{9}-\frac{7}{9})+(\frac{3}{5}+\frac{3}{5})$
$=0+\frac{6}{5}$
$=\frac{6}{5}$
6. $12\frac{4}{5}-(8\frac{4}{5}+3\frac{1}{4})$
$=12\frac{4}{5}-8\frac{4}{5}-3\frac{1}{4}$
$=4-3\frac{1}{4}$
$=\frac{3}{4}$
$=1-(\frac{16}{18}-\frac{9}{18})$
$=1-\frac{7}{18}$
$=\frac{11}{18}$
2. $\frac{8}{9}-\frac{5}{13}+\frac{1}{9}$
$=(\frac{8}{9}+\frac{1}{9})-\frac{5}{13}$
$=1-\frac{5}{13}$
$=\frac{8}{13}$
3. $\frac{2}{5}+\frac{4}{11}+\frac{7}{11}+\frac{8}{5}$
$=(\frac{2}{5}+\frac{8}{5})+(\frac{4}{11}+\frac{7}{11})$
$=2+1$
$=3$
4. $\frac{11}{16}+\frac{3}{10}+\frac{5}{16}-\frac{1}{10}$
$=(\frac{11}{16}+\frac{5}{16})+(\frac{3}{10}-\frac{1}{10})$
$=1+\frac{2}{10}$
$=1+\frac{1}{5}$
$=1\frac{1}{5}$
5. $\frac{7}{9}+\frac{3}{5}-(\frac{7}{9}-\frac{3}{5})$
$=\frac{7}{9}+\frac{3}{5}-\frac{7}{9}+\frac{3}{5}$
$=(\frac{7}{9}-\frac{7}{9})+(\frac{3}{5}+\frac{3}{5})$
$=0+\frac{6}{5}$
$=\frac{6}{5}$
6. $12\frac{4}{5}-(8\frac{4}{5}+3\frac{1}{4})$
$=12\frac{4}{5}-8\frac{4}{5}-3\frac{1}{4}$
$=4-3\frac{1}{4}$
$=\frac{3}{4}$
查看更多完整答案,请扫码查看


