《2025年暑期升级训练五年级数学人教版浙江教育出版社》

1. 有两个同样大小的长方体,长方体的长、宽、高分别是5厘米,4厘米,3厘米,把它们拼成一个大长方体。拼成的大长方体的表面积最大是多少平方厘米？

答案： 解：要使拼成的大长方体表面积最大，需将两个小长方体最小的面拼在一起。
小长方体各面面积：
$5×4 = 20$（平方厘米），$5×3 = 15$（平方厘米），$4×3 = 12$（平方厘米），最小面为$4×3$。
拼成后的大长方体长：$5×2 = 10$（厘米），宽4厘米，高3厘米。
表面积：$(10×4 + 10×3 + 4×3)×2$
$=(40 + 30 + 12)×2$
$=82×2$
$=164$（平方厘米）
答：拼成的大长方体的表面积最大是164平方厘米。

2. 一个长方体,如果长增加2厘米,那么体积增加40立方厘米；如果宽增加3厘米,那么体积增加90立方厘米；如果高增加4厘米,那么体积增加96立方厘米。原来这个长方体的表面积是多少平方厘米？

答案： $(40÷2 + 90÷3 + 96÷4)×2 = 148$(平方厘米)
解析：根据题意可知，一个长方体，如果长增加 2 厘米，那么体积增加 40 立方厘米，即宽与高的乘积是$40÷2 = 20$(平方厘米)；如果宽增加 3 厘米，那么体积增加 90 立方厘米，即长与高的乘积是$90÷3 = 30$(平方厘米)；如果高增加 4 厘米，那么体积增加 96 立方厘米，即长与宽的乘积是$96÷4 = 24$(平方厘米)。最后根据长方体的表面积计算公式进行解答。

3. 一个长方体,如果高增加3厘米,那么它就变成一个正方体,此时表面积就增加48平方厘米。原来长方体的表面积是多少平方厘米？

答案： $48÷4 = 12$(平方厘米) $12÷3 = 4$(厘米) $4 - 3 = 1$(厘米) $4×1×4 + 4×4×2 = 48$(平方厘米)
解析：根据题意可知，一个长方体，如果高增加 3 厘米，那么它就变成一个正方体，说明长和宽相等，且比高长 3 厘米，因此表面积增加的 48 平方厘米是 4 个同样的长方形的面积之和。可以先求出 1 个长方形的面积是$48÷4 = 12$(平方厘米)，再求出长方体的长(宽)是$12÷3 = 4$(厘米)，由于长(宽)比高长 3 厘米，故高是$4 - 3 = 1$(厘米)，从而可以求出原来长方体的表面积。

4. 从一个棱长为4厘米的正方体表面挖掉一个棱长为1厘米的小正方体,有几种方法？挖掉小正方体后,剩余物体的表面积是多少？

答案： 有三种方法：
①从顶点上挖掉小正方体，剩余物体的表面积是$4×4×6=96$（平方厘米）；
②从棱上挖掉小正方体，剩余物体的表面积是$4×4×6 + 1×1×2=98$（平方厘米）；
③从面的中间挖掉小正方体，剩余物体的表面积是$4×4×6 + 1×1×4=100$（平方厘米）。

5. 有4个棱长都是2分米的正方体礼品盒,现在把它们用包装纸包装,有下面两种方案(如图)。哪种方案比较节省包装纸？至少需要多少平方分米的包装纸？(损耗忽略不计)

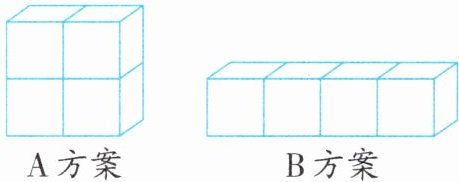
A方案比较节省包装纸，至少需要64平方分米的包装纸。

答案： A方案：
长：$2×2 = 4$（分米），宽：$2×2 = 4$（分米），高：2分米
表面积：$2×(4×4 + 4×2 + 4×2)$
$= 2×(16 + 8 + 8)$
$= 2×32$
$= 64$（平方分米）
B方案：
长：$2×4 = 8$（分米），宽：2分米，高：2分米
表面积：$2×(8×2 + 8×2 + 2×2)$
$= 2×(16 + 16 + 4)$
$= 2×36$
$= 72$（平方分米）
$64＜72$
A方案比较节省包装纸，至少需要64平方分米的包装纸。