例1 一个长方体的长、宽、高分别是6厘米,5厘米和4厘米。若把它切割成三个体积相等的小长方体,则三个小长方体表面积的和最大是多少平方厘米?
点拨:根据长方体切割成小长方体的特点可知,要使切割后的三个小长方体表面积的和最大,可以平行于原来长方体面积最大的面进行切割(如下图),这样表面积就会增加4个原来长方体的最大面的面积。
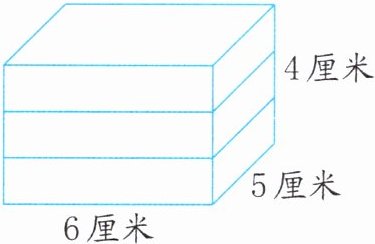
解答:
点拨:根据长方体切割成小长方体的特点可知,要使切割后的三个小长方体表面积的和最大,可以平行于原来长方体面积最大的面进行切割(如下图),这样表面积就会增加4个原来长方体的最大面的面积。

解答:
答案:
$(6×5 + 6×4 + 5×4)×2 = 148$(平方厘米)
$6×5×4 = 120$(平方厘米) $148 + 120 = 268$(平方厘米)
$6×5×4 = 120$(平方厘米) $148 + 120 = 268$(平方厘米)
例2 如图,一个长方体长40cm,横截面是正方形,如果将它的长增加5cm,那么它的表面积就增加$80cm^2。$原来这个长方体的表面积是多少平方厘米?

点拨:长方体的长增加5cm,就相当于拼接了一个和原来长方体等宽、等高的小长方体。新长方体的表面积比原来的长方体增加了小长方体上、下、前、后4个面的面积和,因为横截面是正方形,所以小长方体的宽和高相等,即小长方体上、下、前、后4个面的面积均相等,据此可以先求出小长方体的宽和高,即原来长方体的宽和高。
解答:

点拨:长方体的长增加5cm,就相当于拼接了一个和原来长方体等宽、等高的小长方体。新长方体的表面积比原来的长方体增加了小长方体上、下、前、后4个面的面积和,因为横截面是正方形,所以小长方体的宽和高相等,即小长方体上、下、前、后4个面的面积均相等,据此可以先求出小长方体的宽和高,即原来长方体的宽和高。
解答:
答案:
解:
增加的每个侧面面积:$80÷4 = 20(cm^{2})$
横截面正方形边长:$20÷5 = 4(cm)$
原来长方体表面积:$4×4×2 + 40×4×4 = 32 + 640 = 672(cm^{2})$
答:原来这个长方体的表面积是$672$平方厘米。
增加的每个侧面面积:$80÷4 = 20(cm^{2})$
横截面正方形边长:$20÷5 = 4(cm)$
原来长方体表面积:$4×4×2 + 40×4×4 = 32 + 640 = 672(cm^{2})$
答:原来这个长方体的表面积是$672$平方厘米。
查看更多完整答案,请扫码查看


