2025年奔跑吧少年九年级数学全一册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年九年级数学全一册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如图所示为二次函数$y= -(x-3)^{2}+4$的图象,当$0≤x≤4$时,该函数(
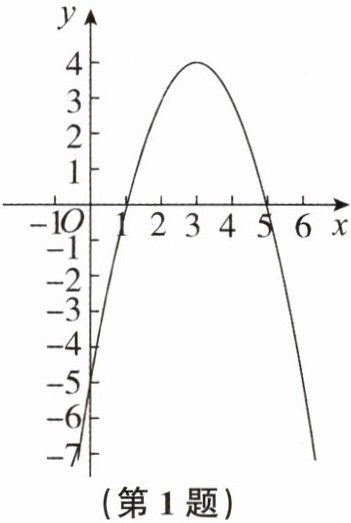
A. 有最小值0,有最大
B. 只有最大值4,无最小值
C. 有最小值-5,有最大值4
D. 有最小值-4,有最大值4
C
)
A. 有最小值0,有最大
B. 只有最大值4,无最小值
C. 有最小值-5,有最大值4
D. 有最小值-4,有最大值4
答案:
C
2. 将一根长2m的铁丝首尾相接围成矩形,则围成的矩形的面积最大是(
A. $\frac {1}{4}m^{2}$
B. $\frac {1}{3}m^{2}$
C. $\frac {1}{2}m^{2}$
D. $1m^{2}$
A
)A. $\frac {1}{4}m^{2}$
B. $\frac {1}{3}m^{2}$
C. $\frac {1}{2}m^{2}$
D. $1m^{2}$
答案:
A
3. 已知两个数的差是16,设被减数是x,则这两个数的积$y= $
$ x ^ { 2 } - 16 x $
(用含x的代数式表示),y的最小值是$ - 64 $
.
答案:
$ x ^ { 2 } - 16 x $ $ - 64 $
4. 已知二次函数$y= x^{2}-4x+3$,当自变量满足$-1≤x≤3$时,y的最大值为
8
,最小值为-1
.
答案:
$ 8 $ $ - 1 $
5. 酶是一种生物催化剂,其催化能力称为活性,活性越高,催化反应越快,研究发现酶的活性与温度有密切关系.已知某种酶在一定温度范围内,其活性y(U)与温度x(℃)的关系可以近似用函数$y= -\frac {1}{2}x^{2}+30x+1200$表示,要使其催化反应最快,则温度应保持在
30
℃.
答案:
$ 30 $
6. 已知直角三角形的两直角边之和为6,则斜边长的最小值是
$ 3 \sqrt { 2 } $
.
答案:
$ 3 \sqrt { 2 } $
7. 用长为8m的铝合金条制成如图所示形状的矩形窗框,使窗户的透光面积最大,

则这个窗户的最大透光面积是(第7题)

则这个窗户的最大透光面积是(第7题)
$\frac{8}{3}$
$m^{2}$(铝合金条遮光部分忽略不计).
答案:
$ \frac { 8 } { 3 } $
8. 求下列二次函数的最大值或最小值.
(1)$y= x^{2}+10x-7$.
(2)$y= -x^{2}+3x+2$.
(1)$y= x^{2}+10x-7$.
(2)$y= -x^{2}+3x+2$.
答案:
$(1)$ 求$y = x^{2}+10x - 7$的最值
解:对于二次函数$y=ax^{2}+bx+c$($a\neq0$),其对称轴公式为$x = -\frac{b}{2a}$,当$a\gt0$时,函数开口向上,在对称轴处取得最小值;当$a\lt0$时,函数开口向下,在对称轴处取得最大值。
在$y = x^{2}+10x - 7$中,$a = 1$,$b = 10$,$c = -7$。
因为$a = 1\gt0$,所以函数开口向上,有最小值。
对称轴$x=-\frac{b}{2a}=-\frac{10}{2×1}=-5$。
把$x = -5$代入函数$y = x^{2}+10x - 7$得:
$y=(-5)^{2}+10×(-5)-7$
$=25 - 50 - 7$
$=-32$。
$(2)$ 求$y=-x^{2}+3x + 2$的最值
解:在$y=-x^{2}+3x + 2$中,$a=-1$,$b = 3$,$c = 2$。
因为$a=-1\lt0$,所以函数开口向下,有最大值。
对称轴$x = -\frac{b}{2a}=-\frac{3}{2×(-1)}=\frac{3}{2}$。
把$x=\frac{3}{2}$代入函数$y=-x^{2}+3x + 2$得:
$y=-\left(\frac{3}{2}\right)^{2}+3×\frac{3}{2}+2$
$=-\frac{9}{4}+\frac{9}{2}+2$
$=-\frac{9}{4}+\frac{18}{4}+\frac{8}{4}$
$=\frac{-9 + 18+8}{4}=\frac{17}{4}$。
综上,$(1)$ $y = x^{2}+10x - 7$有最小值$-32$;$(2)$ $y=-x^{2}+3x + 2$有最大值$\boldsymbol{\frac{17}{4}}$。
解:对于二次函数$y=ax^{2}+bx+c$($a\neq0$),其对称轴公式为$x = -\frac{b}{2a}$,当$a\gt0$时,函数开口向上,在对称轴处取得最小值;当$a\lt0$时,函数开口向下,在对称轴处取得最大值。
在$y = x^{2}+10x - 7$中,$a = 1$,$b = 10$,$c = -7$。
因为$a = 1\gt0$,所以函数开口向上,有最小值。
对称轴$x=-\frac{b}{2a}=-\frac{10}{2×1}=-5$。
把$x = -5$代入函数$y = x^{2}+10x - 7$得:
$y=(-5)^{2}+10×(-5)-7$
$=25 - 50 - 7$
$=-32$。
$(2)$ 求$y=-x^{2}+3x + 2$的最值
解:在$y=-x^{2}+3x + 2$中,$a=-1$,$b = 3$,$c = 2$。
因为$a=-1\lt0$,所以函数开口向下,有最大值。
对称轴$x = -\frac{b}{2a}=-\frac{3}{2×(-1)}=\frac{3}{2}$。
把$x=\frac{3}{2}$代入函数$y=-x^{2}+3x + 2$得:
$y=-\left(\frac{3}{2}\right)^{2}+3×\frac{3}{2}+2$
$=-\frac{9}{4}+\frac{9}{2}+2$
$=-\frac{9}{4}+\frac{18}{4}+\frac{8}{4}$
$=\frac{-9 + 18+8}{4}=\frac{17}{4}$。
综上,$(1)$ $y = x^{2}+10x - 7$有最小值$-32$;$(2)$ $y=-x^{2}+3x + 2$有最大值$\boldsymbol{\frac{17}{4}}$。
9. 如图,已知$//ogram ABCD$的周长为16,$∠D= 30^{\circ }$.设$AB= x,//ogram ABCD$的面积为y,求y关于x的函数表达式及自变量x的取值范围.
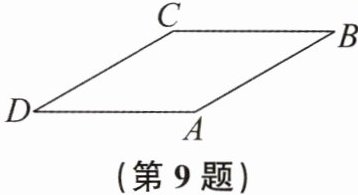

答案:
$ y = - \frac { 1 } { 2 } x ^ { 2 } + 4 x ( 0 < x < 8 ) $.
查看更多完整答案,请扫码查看


