2025年奔跑吧少年九年级数学全一册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年九年级数学全一册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
10. 如图所示为二次函数$y= ax^{2}+bx+c$的部分图象,由图象可知关于x的不等式$ax^{2}+bx+c<0$的解是(
A. $-1<x<5$
B. $x>5$
C. $0<x<5$
D. $x<-1或x>5$
D
)A. $-1<x<5$
B. $x>5$
C. $0<x<5$
D. $x<-1或x>5$
答案:
D
11. 如图所示为根据某拱桥形状建立的平面直角坐标系,从中得到函数$y= -\frac{1}{25}x^{2}$。正常水位时水面宽$AB= 30m$,当水位上升5m时,水面宽CD为
20
m。
答案:
20
12. 已知,抛物线$y= x^{2}+(m-1)x+(m-2)$(m为常数)。
(1)求证:无论m为何值,抛物线与x轴总有公共点。
(2)若抛物线的顶点在x轴上,求m的值。
(3)若抛物线与x轴的两个交点之间的距离为4,求m的值。
(1)求证:无论m为何值,抛物线与x轴总有公共点。
(2)若抛物线的顶点在x轴上,求m的值。
(3)若抛物线与x轴的两个交点之间的距离为4,求m的值。
答案:
$(1)$ 证明抛物线与$x$轴总有公共点
对于抛物线$y = ax^{2}+bx + c$($a\neq0$),其判别式$\Delta=b^{2}-4ac$。
在抛物线$y=x^{2}+(m - 1)x+(m - 2)$中,$a = 1$,$b=m - 1$,$c=m - 2$。
则$\Delta=(m - 1)^{2}-4×1×(m - 2)$
$=m^{2}-2m + 1-4m + 8$
$=m^{2}-6m + 9$
$=(m - 3)^{2}$。
因为$(m - 3)^{2}\geq0$,即$\Delta\geq0$。
所以无论$m$为何值,抛物线与$x$轴总有公共点。
$(2)$ 求$m$的值(顶点在$x$轴上)
对于抛物线$y=ax^{2}+bx + c$($a\neq0$),其顶点纵坐标为$y=\frac{4ac - b^{2}}{4a}$。
因为抛物线顶点在$x$轴上,所以顶点纵坐标为$0$,即$\frac{4×1×(m - 2)-(m - 1)^{2}}{4×1}=0$。
由$(1)$知$4(m - 2)-(m - 1)^{2}=0$,也就是$-(m - 3)^{2}=0$。
解得$m = 3$。
$(3)$ 求$m$的值(两交点距离为$4$)
设抛物线与$x$轴的两个交点的横坐标分别为$x_{1}$,$x_{2}$。
根据韦达定理,对于$ax^{2}+bx + c = 0$($a\neq0$),$x_{1}+x_{2}=-\frac{b}{a}$,$x_{1}x_{2}=\frac{c}{a}$。
对于方程$x^{2}+(m - 1)x+(m - 2)=0$,$x_{1}+x_{2}=-(m - 1)=1 - m$,$x_{1}x_{2}=m - 2$。
已知$\vert x_{1}-x_{2}\vert = 4$,根据$(x_{1}-x_{2})^{2}=(x_{1}+x_{2})^{2}-4x_{1}x_{2}$。
则$(1 - m)^{2}-4(m - 2)=16$。
展开得$1-2m+m^{2}-4m + 8 = 16$。
即$m^{2}-6m - 7 = 0$。
因式分解得$(m - 7)(m+1)=0$。
解得$m = 7$或$m=-1$。
综上,答案依次为:$(1)$ 证明见上述过程;$(2)$$\boldsymbol{m = 3}$;$(3)$$\boldsymbol{m = 7}$或$\boldsymbol{m=-1}$。
对于抛物线$y = ax^{2}+bx + c$($a\neq0$),其判别式$\Delta=b^{2}-4ac$。
在抛物线$y=x^{2}+(m - 1)x+(m - 2)$中,$a = 1$,$b=m - 1$,$c=m - 2$。
则$\Delta=(m - 1)^{2}-4×1×(m - 2)$
$=m^{2}-2m + 1-4m + 8$
$=m^{2}-6m + 9$
$=(m - 3)^{2}$。
因为$(m - 3)^{2}\geq0$,即$\Delta\geq0$。
所以无论$m$为何值,抛物线与$x$轴总有公共点。
$(2)$ 求$m$的值(顶点在$x$轴上)
对于抛物线$y=ax^{2}+bx + c$($a\neq0$),其顶点纵坐标为$y=\frac{4ac - b^{2}}{4a}$。
因为抛物线顶点在$x$轴上,所以顶点纵坐标为$0$,即$\frac{4×1×(m - 2)-(m - 1)^{2}}{4×1}=0$。
由$(1)$知$4(m - 2)-(m - 1)^{2}=0$,也就是$-(m - 3)^{2}=0$。
解得$m = 3$。
$(3)$ 求$m$的值(两交点距离为$4$)
设抛物线与$x$轴的两个交点的横坐标分别为$x_{1}$,$x_{2}$。
根据韦达定理,对于$ax^{2}+bx + c = 0$($a\neq0$),$x_{1}+x_{2}=-\frac{b}{a}$,$x_{1}x_{2}=\frac{c}{a}$。
对于方程$x^{2}+(m - 1)x+(m - 2)=0$,$x_{1}+x_{2}=-(m - 1)=1 - m$,$x_{1}x_{2}=m - 2$。
已知$\vert x_{1}-x_{2}\vert = 4$,根据$(x_{1}-x_{2})^{2}=(x_{1}+x_{2})^{2}-4x_{1}x_{2}$。
则$(1 - m)^{2}-4(m - 2)=16$。
展开得$1-2m+m^{2}-4m + 8 = 16$。
即$m^{2}-6m - 7 = 0$。
因式分解得$(m - 7)(m+1)=0$。
解得$m = 7$或$m=-1$。
综上,答案依次为:$(1)$ 证明见上述过程;$(2)$$\boldsymbol{m = 3}$;$(3)$$\boldsymbol{m = 7}$或$\boldsymbol{m=-1}$。
13. 一个横截面为抛物线形的大棚,有关尺寸如图①。已知大棚横截面最高点到地面的距离为2m,两端触地点A,B相距5m。
(1)以点A为坐标原点,水平向右为x轴正方向,竖直向上为y轴正方向构建平面直角坐标系,求此抛物线的函数表达式(不需要求自变量的取值范围)。
(2)一位身高1.60m的菜农,若要在大棚内站直行走,求此菜农在横截面内横向活动范围是多少米。
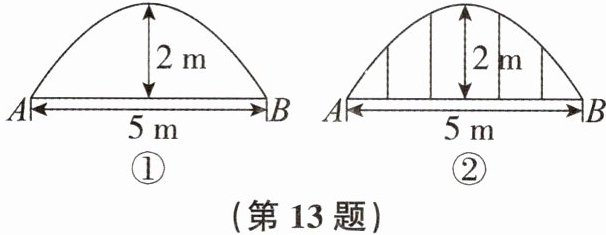
(1)以点A为坐标原点,水平向右为x轴正方向,竖直向上为y轴正方向构建平面直角坐标系,求此抛物线的函数表达式(不需要求自变量的取值范围)。
(2)一位身高1.60m的菜农,若要在大棚内站直行走,求此菜农在横截面内横向活动范围是多少米。

答案:
1. (1)
已知抛物线的顶点坐标为$(\frac{5}{2},2)$,设抛物线的函数表达式为$y = a(x - h)^{2}+k$($a\neq0$),这里$h=\frac{5}{2}$,$k = 2$,则$y=a(x-\frac{5}{2})^{2}+2$。
因为抛物线过点$A(0,0)$,把$x = 0$,$y = 0$代入$y=a(x-\frac{5}{2})^{2}+2$得:
$0=a(0 - \frac{5}{2})^{2}+2$。
即$0=\frac{25}{4}a+2$,移项可得$\frac{25}{4}a=-2$,解得$a=-\frac{8}{25}$。
所以抛物线的函数表达式为$y =-\frac{8}{25}(x-\frac{5}{2})^{2}+2$,展开$y =-\frac{8}{25}(x^{2}-5x+\frac{25}{4})+2$,$y=-\frac{8}{25}x^{2}+\frac{8}{5}x$。
2. (2)
当$y = 1.6$时,代入$y=-\frac{8}{25}x^{2}+\frac{8}{5}x$得:
$1.6=-\frac{8}{25}x^{2}+\frac{8}{5}x$。
方程两边同时乘以$25$得:$40=-8x^{2}+40x$。
移项化为标准的一元二次方程形式$8x^{2}-40x + 40 = 0$,两边同时除以$8$得$x^{2}-5x + 5 = 0$。
根据一元二次方程$ax^{2}+bx + c = 0(a = 1,b=-5,c = 5)$的求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$,这里$\Delta=b^{2}-4ac=(-5)^{2}-4×1×5=25 - 20 = 5$。
则$x=\frac{5\pm\sqrt{5}}{2}$。
那么$x_1 - x_2=\vert\frac{5+\sqrt{5}}{2}-\frac{5 - \sqrt{5}}{2}\vert=\sqrt{5}\approx2.24$(米)。
综上,(1)抛物线的函数表达式为$y =-\frac{8}{25}x^{2}+\frac{8}{5}x$;(2)菜农在横截面内横向活动范围约是$2.24$米。
已知抛物线的顶点坐标为$(\frac{5}{2},2)$,设抛物线的函数表达式为$y = a(x - h)^{2}+k$($a\neq0$),这里$h=\frac{5}{2}$,$k = 2$,则$y=a(x-\frac{5}{2})^{2}+2$。
因为抛物线过点$A(0,0)$,把$x = 0$,$y = 0$代入$y=a(x-\frac{5}{2})^{2}+2$得:
$0=a(0 - \frac{5}{2})^{2}+2$。
即$0=\frac{25}{4}a+2$,移项可得$\frac{25}{4}a=-2$,解得$a=-\frac{8}{25}$。
所以抛物线的函数表达式为$y =-\frac{8}{25}(x-\frac{5}{2})^{2}+2$,展开$y =-\frac{8}{25}(x^{2}-5x+\frac{25}{4})+2$,$y=-\frac{8}{25}x^{2}+\frac{8}{5}x$。
2. (2)
当$y = 1.6$时,代入$y=-\frac{8}{25}x^{2}+\frac{8}{5}x$得:
$1.6=-\frac{8}{25}x^{2}+\frac{8}{5}x$。
方程两边同时乘以$25$得:$40=-8x^{2}+40x$。
移项化为标准的一元二次方程形式$8x^{2}-40x + 40 = 0$,两边同时除以$8$得$x^{2}-5x + 5 = 0$。
根据一元二次方程$ax^{2}+bx + c = 0(a = 1,b=-5,c = 5)$的求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$,这里$\Delta=b^{2}-4ac=(-5)^{2}-4×1×5=25 - 20 = 5$。
则$x=\frac{5\pm\sqrt{5}}{2}$。
那么$x_1 - x_2=\vert\frac{5+\sqrt{5}}{2}-\frac{5 - \sqrt{5}}{2}\vert=\sqrt{5}\approx2.24$(米)。
综上,(1)抛物线的函数表达式为$y =-\frac{8}{25}x^{2}+\frac{8}{5}x$;(2)菜农在横截面内横向活动范围约是$2.24$米。
14. 二次函数$y= ax^{2}-2ax+c的图象过点(0,-1)$,其部分图象如图所示,则关于x的方程$ax^{2}-2ax+c= -1$的正数解为______。
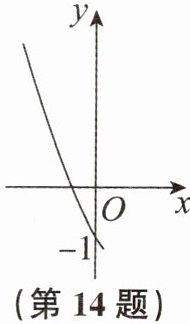

$ x = 2 $
答案:
$ x = 2 $
查看更多完整答案,请扫码查看


