2025年奔跑吧少年九年级数学全一册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年九年级数学全一册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
11. 如图,在扇形AOB中,半径$OA= 3$,C是OA上一点,且$OC= CA$,连结BC. 若$BC⊥AC$,则$\widehat {AB}$的长为(
A. $\frac {π}{6}$
B. $\frac {π}{3}$
C. $\frac {π}{2}$
D. $π$
D
)A. $\frac {π}{6}$
B. $\frac {π}{3}$
C. $\frac {π}{2}$
D. $π$
答案:
D
12. 如图,$△ABC内接于\odot O$,$∠B= 65^{\circ }$,$∠C= 70^{\circ }$. 若$BC= 2\sqrt {2}$,则$\widehat {BC}$的长为(
A. $π$
B. $\sqrt {2}π$
C. $2π$
D. $2\sqrt {2}π$
A
)A. $π$
B. $\sqrt {2}π$
C. $2π$
D. $2\sqrt {2}π$
答案:
A
13. 如图,正六边形ABCDEF的边长为3,且内接于$\odot O$,则劣弧AB的长为
$\pi$
.
答案:
$ \pi $
14. 传统服饰日益受到关注,马面裙是明清时期女子的主要裙式之一,可以近似地看做扇环(如图),其中$\widehat {AD}的长度为\frac {1}{3}πm$,$\widehat {BC}的长度为\frac {3}{5}πm$,圆心角$∠AOD= 60^{\circ }$,则裙长AB为
0.8
m.
答案:
0.8
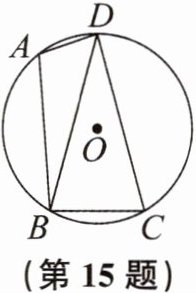
15. 如图,已知四边形ABCD内接于$\odot O$,连结BD,$∠BAD= 105^{\circ }$,$∠DBC= 75^{\circ }$.
(1)求证:$BD= CD$.
(2)若$\odot O$的半径为3,求$\widehat {BC}$的长.
(1)求证:$BD= CD$.
(2)若$\odot O$的半径为3,求$\widehat {BC}$的长.

答案:
1. (1)证明:
因为四边形$ABCD$内接于$\odot O$,根据圆内接四边形的性质:$\angle BAD+\angle BCD = 180^{\circ}$(圆内接四边形对角互补)。
已知$\angle BAD = 105^{\circ}$,则$\angle BCD=180^{\circ}-\angle BAD$,即$\angle BCD = 180 - 105=75^{\circ}$。
又因为$\angle DBC = 75^{\circ}$,所以$\angle BCD=\angle DBC$。
根据等腰三角形的判定(等角对等边),在$\triangle BCD$中,可得$BD = CD$。
2. (2)解:
因为$\angle BCD=\angle DBC = 75^{\circ}$,根据圆周角定理:同弧所对的圆心角是圆周角的$2$倍。
设圆心为$O$,$\angle BOC$是圆心角,$\angle BDC$是圆周角,$\angle BDC=\angle BAC$(同弧$\overset{\frown}{BC}$所对的圆周角相等)。
在$\triangle BCD$中,$\angle BDC=180^{\circ}-\angle DBC-\angle BCD=180 - 75-75 = 30^{\circ}$。
所以$\angle BOC = 2\angle BDC$(同弧所对的圆心角是圆周角的$2$倍),则$\angle BOC=60^{\circ}$。
已知$\odot O$的半径$r = 3$,根据弧长公式$l=\frac{n\pi r}{180}$(其中$n$是圆心角的度数,$r$是半径)。
对于$\overset{\frown}{BC}$,$n = 60^{\circ}$,$r = 3$,则$l_{\overset{\frown}{BC}}=\frac{60\pi×3}{180}=\pi$。
综上,(1)得证$BD = CD$;(2)$\overset{\frown}{BC}$的长为$\pi$。
因为四边形$ABCD$内接于$\odot O$,根据圆内接四边形的性质:$\angle BAD+\angle BCD = 180^{\circ}$(圆内接四边形对角互补)。
已知$\angle BAD = 105^{\circ}$,则$\angle BCD=180^{\circ}-\angle BAD$,即$\angle BCD = 180 - 105=75^{\circ}$。
又因为$\angle DBC = 75^{\circ}$,所以$\angle BCD=\angle DBC$。
根据等腰三角形的判定(等角对等边),在$\triangle BCD$中,可得$BD = CD$。
2. (2)解:
因为$\angle BCD=\angle DBC = 75^{\circ}$,根据圆周角定理:同弧所对的圆心角是圆周角的$2$倍。
设圆心为$O$,$\angle BOC$是圆心角,$\angle BDC$是圆周角,$\angle BDC=\angle BAC$(同弧$\overset{\frown}{BC}$所对的圆周角相等)。
在$\triangle BCD$中,$\angle BDC=180^{\circ}-\angle DBC-\angle BCD=180 - 75-75 = 30^{\circ}$。
所以$\angle BOC = 2\angle BDC$(同弧所对的圆心角是圆周角的$2$倍),则$\angle BOC=60^{\circ}$。
已知$\odot O$的半径$r = 3$,根据弧长公式$l=\frac{n\pi r}{180}$(其中$n$是圆心角的度数,$r$是半径)。
对于$\overset{\frown}{BC}$,$n = 60^{\circ}$,$r = 3$,则$l_{\overset{\frown}{BC}}=\frac{60\pi×3}{180}=\pi$。
综上,(1)得证$BD = CD$;(2)$\overset{\frown}{BC}$的长为$\pi$。
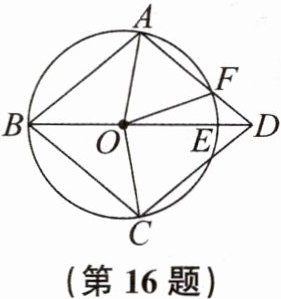
16. 如图,在$\odot O$上依次有A,B,C三点,BO的延长线交$\odot O$于点E,$\widehat {AE}= \widehat {CE}$,过点C作$CD// AB$交BE的延长线于点D,连结AD交$\odot O$于点F.
(1)求证:四边形ABCD是菱形.
(2)连结OA,OF,OC,若$∠AOF= 3∠FOD$,且$AF= 3$,求$\widehat {CF}$的长.
(1)求证:四边形ABCD是菱形.
(2)连结OA,OF,OC,若$∠AOF= 3∠FOD$,且$AF= 3$,求$\widehat {CF}$的长.

答案:
1. (1)证明:
因为$\widehat{AE}=\widehat{CE}$,所以$\angle ABE = \angle CBE$(同圆或等圆中,等弧所对的圆周角相等)。
又因为$CD// AB$,所以$\angle ABD=\angle CDB$,则$\angle CBE=\angle CDB$,所以$BC = CD$。
因为$BE$是$\odot O$的直径,$\widehat{AE}=\widehat{CE}$,所以$AB = BC$(同圆或等圆中,等弧所对的弦相等)。
因为$CD// AB$,$AB = BC$,$BC = CD$,所以四边形$ABCD$是平行四边形(一组对边平行且相等的四边形是平行四边形),又$AB = BC$,所以平行四边形$ABCD$是菱形(一组邻边相等的平行四边形是菱形)。
2. (2)解:长为$\frac{5π}3$
因为$\widehat{AE}=\widehat{CE}$,所以$\angle ABE = \angle CBE$(同圆或等圆中,等弧所对的圆周角相等)。
又因为$CD// AB$,所以$\angle ABD=\angle CDB$,则$\angle CBE=\angle CDB$,所以$BC = CD$。
因为$BE$是$\odot O$的直径,$\widehat{AE}=\widehat{CE}$,所以$AB = BC$(同圆或等圆中,等弧所对的弦相等)。
因为$CD// AB$,$AB = BC$,$BC = CD$,所以四边形$ABCD$是平行四边形(一组对边平行且相等的四边形是平行四边形),又$AB = BC$,所以平行四边形$ABCD$是菱形(一组邻边相等的平行四边形是菱形)。
2. (2)解:长为$\frac{5π}3$
查看更多完整答案,请扫码查看


