2025年奔跑吧少年九年级数学全一册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年九年级数学全一册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
11. 已知一次函数$y= kx+b(k≠0)$,若k从2,-3中随机取一个值,b从1,-1,-2中随机取一个值,则该一次函数的图象经过第二、三、四象限的概率是 (
A. $\frac {1}{3}$
B. $\frac {2}{3}$
C. $\frac {1}{6}$
D. $\frac {5}{6}$
A
)A. $\frac {1}{3}$
B. $\frac {2}{3}$
C. $\frac {1}{6}$
D. $\frac {5}{6}$
答案:
A
12. 在如图所示的四个转盘中,C,D转盘被分成8等份,若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是 (
A
)
答案:
A
13. 有5张看上去没有差别的卡片,上面分别写着数字1,2,3,4,5,随机抽取3张,用抽到的三个数字作为边长,恰能构成三角形的概率是 (
A. $\frac {3}{10}$
B. $\frac {3}{20}$
C. $\frac {7}{20}$
D. $\frac {7}{10}$
A
)A. $\frac {3}{10}$
B. $\frac {3}{20}$
C. $\frac {7}{20}$
D. $\frac {7}{10}$
答案:
A
14. 某志愿小组有五名翻译,其中一名只会翻译阿拉伯语,三名只会翻译英语,还有一名这两种语言都会翻译,若从中随机挑选两名组成一组,则该组能够翻译上述两种语言的概率是
$\frac{7}{10}$
.
答案:
$\frac{7}{10}$
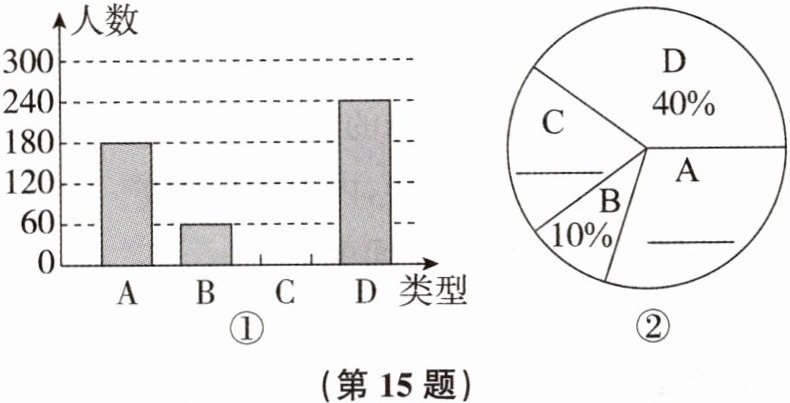
15. 2024年“五一”期间,旅游景点人头攒动,热闹非凡,某市文化和旅游局选择宝鼎、天池湖、百万玫瑰园、华蓥山石林(以下分别用A,B,C,D表示)四个景区,对本次“五一”假期的游客人数进行了抽样调查,并将调查情况绘制成如下不完整的两幅统计图.
(1)本次参加抽样调查的游客有多少人?
(2)请将两幅不完整的统计图补充完整.
(3)若某游客随机选择A,B,C,D四个景区中的两个,请用列表或画树状图的方法求他恰好选择A和D的概率.
(1)本次参加抽样调查的游客有多少人?
(2)请将两幅不完整的统计图补充完整.
(3)若某游客随机选择A,B,C,D四个景区中的两个,请用列表或画树状图的方法求他恰好选择A和D的概率.

答案:
$(1)$计算本次参加抽样调查的游客人数
已知$D$景区人数为$240$人,且$D$景区人数占总人数的$40\%$。
设本次参加抽样调查的游客有$x$人,根据公式$\frac{部分量}{总量}=所占比例$,可得$\frac{240}{x}=40\%=\frac{40}{100}$,即$x = \frac{240}{\frac{40}{100}}=240×\frac{100}{40}=600$(人)。
$(2)$补充统计图
计算$A$、$C$景区人数及$A$、$C$景区人数占比:
$B$景区人数为$60$人,占比$10\%$,$D$景区人数$240$人,占比$40\%$,$A$景区人数为$180$人,则$A$景区人数占比为$\frac{180}{600}×100\% = 30\%$。
$C$景区人数为$600 - 180 - 60 - 240=120$(人),$C$景区人数占比为$\frac{120}{600}× 100\%=20\%$。
补充条形统计图:**在条形统计图中,$C$对应的条形高度为$120$(与纵轴刻度对应)。
补充扇形统计图:**在扇形统计图中,$A$对应的扇形圆心角为$360^{\circ}×30\% = 108^{\circ}$,$C$对应的扇形圆心角为$360^{\circ}×20\%=72^{\circ}$。
$(3)$计算恰好选择$A$和$D$的概率
列表法:
设$A$、$B$、$C$、$D$四个景区,列表如下:
| | $A$ | $B$ | $C$ | $D$ |
| --- | --- | --- | --- | --- |
| $A$ | $(A,A)$ | $(A,B)$ | $(A,C)$ | $(A,D)$ |
| $B$ | $(B,A)$ | $(B,B)$ | $(B,C)$ | $(B,D)$ |
| $C$ | $(C,A)$ | $(C,B)$ | $(C,C)$ | $(C,D)$ |
| $D$ | $(D,A)$ | $(D,B)$ | $(D,C)$ | $(D,D)$ |
从列表中可以看出,一共有$n = 12$种等可能的结果,其中恰好选择$A$和$D$(即$(A,D)$和$(D,A)$)的结果有$m = 2$种。
根据概率公式$P=\frac{m}{n}$,可得$P=\frac{2}{12}=\frac{1}{6}$。
树状图法:
首先从$4$个景区选第一个景区,有$4$种可能,再从剩下$3$个景区选第二个景区,有$3$种可能。
树状图如下:
第一层:$A$、$B$、$C$、$D$;
若第一层选$A$,第二层:$B$、$C$、$D$;
若第一层选$B$,第二层:$A$、$C$、$D$;
若第一层选$C$,第二层:$A$、$B$、$D$;
若第一层选$D$,第二层:$A$、$B$、$C$。
总共的结果数$n=4×3 = 12$种,恰好选$A$和$D$($A$后$D$,$D$后$A$)的结果数$m = 2$种。
根据概率公式$P=\frac{m}{n}$,可得$P=\frac{2}{12}=\frac{1}{6}$。
综上,答案依次为:$(1)$$\boldsymbol{600}$人;$(3)$$\boldsymbol{\frac{1}{6}}$。
已知$D$景区人数为$240$人,且$D$景区人数占总人数的$40\%$。
设本次参加抽样调查的游客有$x$人,根据公式$\frac{部分量}{总量}=所占比例$,可得$\frac{240}{x}=40\%=\frac{40}{100}$,即$x = \frac{240}{\frac{40}{100}}=240×\frac{100}{40}=600$(人)。
$(2)$补充统计图
计算$A$、$C$景区人数及$A$、$C$景区人数占比:
$B$景区人数为$60$人,占比$10\%$,$D$景区人数$240$人,占比$40\%$,$A$景区人数为$180$人,则$A$景区人数占比为$\frac{180}{600}×100\% = 30\%$。
$C$景区人数为$600 - 180 - 60 - 240=120$(人),$C$景区人数占比为$\frac{120}{600}× 100\%=20\%$。
补充条形统计图:**在条形统计图中,$C$对应的条形高度为$120$(与纵轴刻度对应)。
补充扇形统计图:**在扇形统计图中,$A$对应的扇形圆心角为$360^{\circ}×30\% = 108^{\circ}$,$C$对应的扇形圆心角为$360^{\circ}×20\%=72^{\circ}$。
$(3)$计算恰好选择$A$和$D$的概率
列表法:
设$A$、$B$、$C$、$D$四个景区,列表如下:
| | $A$ | $B$ | $C$ | $D$ |
| --- | --- | --- | --- | --- |
| $A$ | $(A,A)$ | $(A,B)$ | $(A,C)$ | $(A,D)$ |
| $B$ | $(B,A)$ | $(B,B)$ | $(B,C)$ | $(B,D)$ |
| $C$ | $(C,A)$ | $(C,B)$ | $(C,C)$ | $(C,D)$ |
| $D$ | $(D,A)$ | $(D,B)$ | $(D,C)$ | $(D,D)$ |
从列表中可以看出,一共有$n = 12$种等可能的结果,其中恰好选择$A$和$D$(即$(A,D)$和$(D,A)$)的结果有$m = 2$种。
根据概率公式$P=\frac{m}{n}$,可得$P=\frac{2}{12}=\frac{1}{6}$。
树状图法:
首先从$4$个景区选第一个景区,有$4$种可能,再从剩下$3$个景区选第二个景区,有$3$种可能。
树状图如下:
第一层:$A$、$B$、$C$、$D$;
若第一层选$A$,第二层:$B$、$C$、$D$;
若第一层选$B$,第二层:$A$、$C$、$D$;
若第一层选$C$,第二层:$A$、$B$、$D$;
若第一层选$D$,第二层:$A$、$B$、$C$。
总共的结果数$n=4×3 = 12$种,恰好选$A$和$D$($A$后$D$,$D$后$A$)的结果数$m = 2$种。
根据概率公式$P=\frac{m}{n}$,可得$P=\frac{2}{12}=\frac{1}{6}$。
综上,答案依次为:$(1)$$\boldsymbol{600}$人;$(3)$$\boldsymbol{\frac{1}{6}}$。
16. 把三张形状、大小相同但画面不同的风景图片,都按照同样的方式剪成相同的三段,然后将上、中、下段分别混合均匀,从三堆图片中随机各抽出一张,求这三张图片恰好组成一张完整风景图片的概率.
答案:
$\frac{1}{9}$.
查看更多完整答案,请扫码查看


