《2025年奔跑吧少年九年级数学全一册浙教版》

10. 如图,将半径为4cm的圆折叠后,圆弧恰好经过圆心O,则$∠AOB$的度数为(A)
A. $120^{\circ }$
B. $100^{\circ }$
C. $150^{\circ }$
D. $140^{\circ }$

答案： A

11. 如图,矩形ABCD为一个正在倒水的水杯的截面图,$AB= 24cm$,杯中水面与CD的交点为E,AE平行于水平面,当水杯底面BC与水平面的夹角为$30^{\circ }$时,杯中水的最大深度为(D)
A. 8cm
B. 12cm
C. $8\sqrt {3}cm$
D. $12\sqrt {3}cm$

答案： D

12. 如图,某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形.已知矩形的宽为2m,高为$2\sqrt {3}m$,则改建后门洞的圆弧长为$\frac{10\pi}{3}$.

答案： $ \frac{10\pi}{3} $

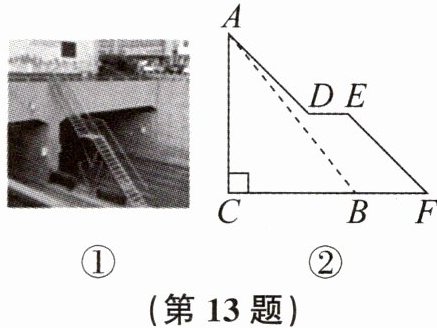
13. 某市为排除隧道安全隐患,根据各段隧道空间情况,在不影响交通的情况下,加装了大小、形状不一的19条人行逃生爬梯.如图①,起初工程师计划修建一段坡角为$50^{\circ }$(即$∠ABC= 50^{\circ },∠BAC= 40^{\circ }$)的爬梯AB,从安全角度再次考虑,工程师对爬梯的设计进行了修改,如图②,修建了AD,EF两段平行的爬梯,并在中间修建了1米的水平平台DE,C,B,F三点共线,小明实地测量后得到AC为4米,CF为5米.
(1)求修改后的爬梯坡角比修改前坡角减缓了多少度.
(2)求修改后爬梯的底部F与修改前爬梯的底部B之间的距离(结果精确到0.1米.参考数据：$sin40^{\circ }\approx 0.64,cos40^{\circ }\approx 0.77,tan40^{\circ }\approx 0.84$).

答案：
(1) $ 5^{\circ} $.
(2)1.6米.

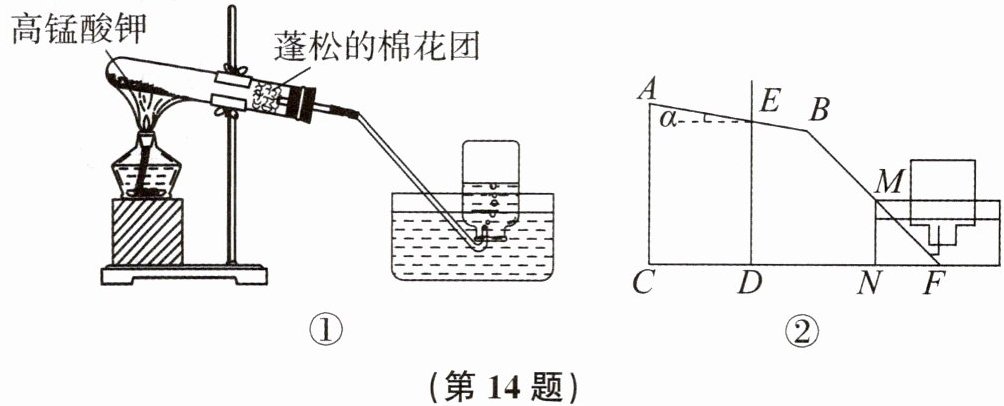
14. 实验是培养学生的创新能力的重要途径之一.如图①所示为小红同学安装的某实验装置,安装要求为试管略向下倾斜,试管夹应固定在距试管口的三分之一处.如图②,已知试管$AB= 24cm,BE= \frac {1}{3}AB$,试管的倾斜角α为$10^{\circ }$.(结果精确到0.1cm.参考数据：$sin10^{\circ }\approx 0.17,cos10^{\circ }\approx 0.98,tan10^{\circ }\approx 0.18$)
(1)求酒精灯与铁架台的水平距离CD的长度.
(2)实验时,当导气管紧贴水槽MN,延长BM交CN的延长线于点F,且$MN⊥CF$(点C,D,N,F在一条直线上),经测得$DE= 27.36cm,MN= 8cm,∠ABM= 145^{\circ }$,求线段DN的长度.

答案：
(1)15.7 cm.
(2)25.8 cm.