《2025年奔跑吧少年九年级数学全一册浙教版》

1. 如果斜坡的坡面的垂直高度$h= \frac {3}{2}m$,水平宽度$l= \frac {\sqrt {3}}{2}m$,那么斜坡的坡角为(C)
A. $30^{\circ }$
B. $45^{\circ }$
C. $60^{\circ }$
D. $75^{\circ }$

答案： C

2. 如图,一辆轿车沿倾斜角为$30^{\circ }$的斜坡向上行驶,若轿车水平方向所经过的距离为50m,则轿车在斜坡上行驶的距离为(C)
A. 100m
B. $25\sqrt {3}m$
C. $\frac {100\sqrt {3}}{3}m$
D. $100\sqrt {3}m$

答案： C

3. 如图,有一斜坡AB,坡顶点B离地面的高BC为15m,斜坡的倾斜角是$∠BAC$.若$tan∠BAC= \frac {3}{5}$,则此斜坡的水平宽度(AC)为(A)
A. 25m
B. 20m
C. 15m
D. 9m

答案： A

4. 如图,在圆中存在一个内接正五边形,如果这个正五边形外接圆的半径是R,那么它的边长为(C)
A. $Rsin36^{\circ }$
B. $Rsin72^{\circ }$
C. $2Rsin36^{\circ }$
D. $2Rsin72^{\circ }$

答案： C

5. 如果一传送带和地面所成斜坡的坡比为$1:3$,它把物体从传送带的最低点A处送到离地面3米高的点B处,那么物体从点A到点B所经过的路程为(D)
A. 9米
B. $\sqrt {10}$米
C. $2\sqrt {10}$米
D. $3\sqrt {10}$米

答案： D

6. 如图,小杰沿着坡比为$1:2.5$的斜坡,从坡底A沿水平方向前进了100m($AB= 100m$)到达C处,那么他上升的高度(BC)是40m.

答案： 40

7. 某人沿着一个斜坡往上走动了5米,他的垂直高度上升了3米,则这个坡的坡比$i=$$ 1:\frac{4}{3} $.

答案： $ 1:\frac{4}{3} $

8. 将一张圆心角为α的扇形纸板按如图所示的方式剪得一个正方形,正方形的边长为5cm,已知$tanα= 1$,求扇形纸板的弧长.

答案： $ \frac{5\sqrt{5}\pi}{4} $ cm.

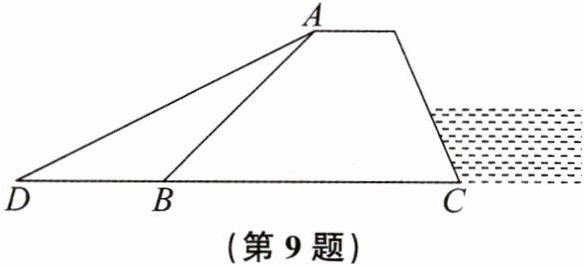
9. 某防洪大堤的横断面如图所示,背水坡的坡面AB的长度为20m,坡比为$1:1$(坡比为坡面的垂直高度与水平宽度的比),汛期来临前要对背水坡进行加固,改造后的背水坡的坡面AD的坡比为$1:2$,求改造后的背水坡AD的长度.

答案： 1. 首先，根据坡比的定义和勾股定理求$AE$和$BE$的长度：
过点$A$作$AE\perp DC$于点$E$。
已知坡面$AB$的坡比$i = 1:1$，即$\frac{AE}{BE}=1$，设$AE = h$，$BE = h$。
在$Rt\triangle ABE$中，根据勾股定理$AB^{2}=AE^{2}+BE^{2}$（$AB = 20m$），由$AB^{2}=h^{2}+h^{2}$，即$20^{2}=2h^{2}$。
解方程$h^{2}=\frac{20^{2}}{2}=200$，得$h = 10\sqrt{2}m$（因为长度为正，舍去负值），所以$AE = 10\sqrt{2}m$。
2. 然后，根据改造后的坡比求$DE$的长度：
因为改造后的背水坡的坡面$AD$的坡比为$1:2$，即$\frac{AE}{DE}=\frac{1}{2}$。
已知$AE = 10\sqrt{2}m$，由$\frac{10\sqrt{2}}{DE}=\frac{1}{2}$，可得$DE = 20\sqrt{2}m$。
3. 最后，在$Rt\triangle ADE$中求$AD$的长度：
在$Rt\triangle ADE$中，根据勾股定理$AD=\sqrt{AE^{2}+DE^{2}}$。
把$AE = 10\sqrt{2}m$，$DE = 20\sqrt{2}m$代入，得$AD=\sqrt{(10\sqrt{2})^{2}+(20\sqrt{2})^{2}}$。
计算$(10\sqrt{2})^{2}+(20\sqrt{2})^{2}=200 + 800=1000$。
所以$AD=\sqrt{1000}=10\sqrt{10}m$。
答：改造后的背水坡$AD$的长度为$10\sqrt{10}m$。