《2025年奔跑吧少年九年级数学全一册浙教版》

1. 若△ABC的每条边长扩大为原来的2倍得△A'B'C',则∠B'的度数与其对应角∠B的度数相比(D)
A. 扩大2倍
B. 缩小2倍
C. 扩大4倍
D. 没有改变

答案： D

2. 已知△ABC的三边长分别为2,5,6. 若要使△DEF∽△ABC,则△DEF的三边长可以是(B)
A. 3,6,7
B. 6,15,18
C. 3,8,9
D. 8,10,12

答案： B

3. 如图,下列所给的三角形中,与△ABC一定相似的是(A)

答案： A

4. 如图,在四个均由16个小正方形组成的正方形网格中,各有一个格点三角形,那么这四个三角形中,形状与其他三个不同的是(A)

答案： A

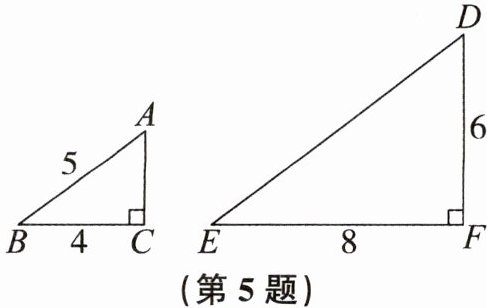
5. 如图,△ABC与△DEF相似(填“相似”或“不相似”).

答案： 相似

6. 在△ABC和△A'B'C'中,有下列条件：①$\frac {AB}{A'B'}= \frac {BC}{B'C'}$；②$\frac {AC}{A'C'}= \frac {BC}{B'C'}$；③∠A= ∠A'；④∠C= ∠C'. 如果从中任取两个条件组成一组,那么能判断△ABC∽△A'B'C'的共有3组.

答案： 3

7. 如图,已知$\frac {AB}{AD}= \frac {BC}{DE}= \frac {AC}{AE}$,试判断∠BAD和∠CAE的大小关系,并说明理由.

答案： 解：因为$\frac{AB}{AD}=\frac{BC}{DE}=\frac{AC}{AE}$，所以$\triangle ABC\sim\triangle ADE$（三边对应成比例的两个三角形相似）。
所以$\angle BAC = \angle DAE$。
又因为$\angle BAD+\angle DAC=\angle BAC$，$\angle CAE+\angle DAC=\angle DAE$，
所以$\angle BAD=\angle CAE$。

8. 如图,△ABC三边长分别为AB= 5cm,BC= 6cm,AC= 4cm,△DEF的三边长分别为DE= 9cm,EF= 7.5cm,DF= 6cm,则△ABC与△DEF是否相似？请说明理由.

答案： 解：
计算两个三角形对应边的比值：
$\frac{AB}{DF}=\frac{5}{6}$；
$\frac{BC}{DE}=\frac{6}{9}=\frac{2}{3}$；
$\frac{AC}{EF}=\frac{4}{7.5}=\frac{8}{15}$。
因为$\frac{5}{6}\neq\frac{2}{3}\neq\frac{8}{15}$，即三边对应不成比例。
所以$\triangle ABC$与$\triangle DEF$不相似。