《2025年奔跑吧少年九年级数学全一册浙教版》

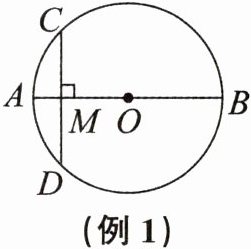
例1 (2024秋·宁波镇海期末改编)如图,AB是$\odot O$的直径,弦$CD⊥AB$,垂足为M.若$CD= BM= 8$,求AM的长.

答案： 2.

跟踪训练1-1 如图,半圆的直径$AB= 4$,点O为圆心,过点O作$OF⊥CD$,交弦CD于点F,交半圆于点E,

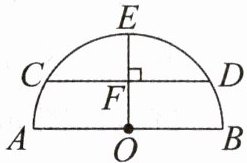
且F为OE的中点,则弦CD的长是 (B)
A. $\sqrt{3}$
B. $2\sqrt{3}$
C. $\sqrt{5}$
D. $2\sqrt{5}$

答案： B

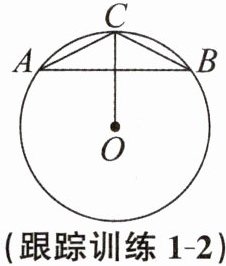
跟踪训练1-2 点A,B,C都在$\odot O$上,且$CA= CB$,若$AB= 8,\odot O$的半径为5,连结CO,求$\triangle ABC$的周长.

答案： $4\sqrt{5}+8$.

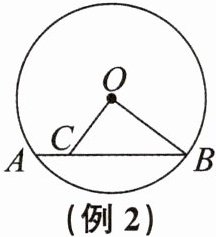
例2 (2024秋·绍兴嵊州期末)如图,$\odot O$的半径为5,C是弦AB上一点.若$AB= 8$,设$OC= x$,则x的取值范围是 (A)

A. $3\leqslant x\leqslant 5$
B. $3\lt x\leqslant 5$
C. $4\leqslant x\leqslant 5$
D. $4\lt x\leqslant 5$

答案： A

跟踪训练2-1 如图,在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点.若AB= 4,CD=2,AB的弦心距等于1,则两个同心圆的半径之比为 (C)
A. $3:2$
B. $\sqrt{5}:2$
C. $\sqrt{5}:\sqrt{2}$
D. $5:4$

答案： C

跟踪训练2-2 在半径为1的$\odot O$中,弦AB,AC的长分别为1和$\sqrt{2}$,则$∠BAC$的度数为$15^{\circ}$或 $105^{\circ}$.

答案： $15^{\circ}$或 $105^{\circ}$

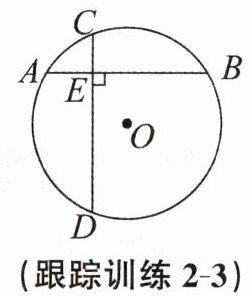
跟踪训练2-3 如图,已知在$\odot O$中,AB,CD两条弦互相垂直于点E,AB被分成$AE= 4cm和BE= 10cm$的两段.
(1)求圆心O到CD的距离.
(2)若$\odot O$的半径为8cm,求CD的长.

答案：
(1) $3\mathrm{cm}$.
(2) $2\sqrt{55}\mathrm{cm}$.