2025年奔跑吧少年九年级数学全一册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年九年级数学全一册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 在$\triangle ABC$中,$D是边BC$的中点,连结$AD$,点$O在AD$上,且$AO:OD = 2:1$,则点$O是\triangle ABC$的(
A. 垂心
B. 重心
C. 外心
D. 内心
B
)A. 垂心
B. 重心
C. 外心
D. 内心
答案:
B
2. 如图,$\triangle ABC \backsim \triangle A_1B_1C_1$,$AD$,$A_1D_1分别是\angle BAC$,$\angle B_1A_1C_1$的平分线,若$\frac{AB}{A_1B_1} = \frac{1}{3}$,则$\frac{AD}{A_1D_1}$的值为(
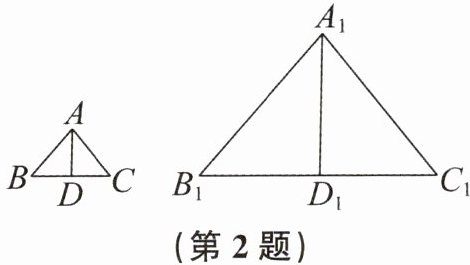
A. 3
B. $\frac{1}{9}$
C. $\frac{1}{3}$
D. 9
C
)
A. 3
B. $\frac{1}{9}$
C. $\frac{1}{3}$
D. 9
答案:
C
3. 若两个相似三角形对应边上的高线长之比为$5:1$,则它们的相似比为(
A. $25:1$
B. $10:1$
C. $5:1$
D. $\sqrt{5}:1$
C
)A. $25:1$
B. $10:1$
C. $5:1$
D. $\sqrt{5}:1$
答案:
C
4. 如图所示的网格由边长相同的小正方形组成,点$A$,$B$,$C$,$D$,$E$,$F$,$G$在小正方形的格点上,则$\triangle ABC$的重心是(
A. 点$D$
B. 点$E$
C. 点$F$
D. 点$G$
A
)A. 点$D$
B. 点$E$
C. 点$F$
D. 点$G$
答案:
A
5. 两个相似三角形的对应中线之比是$4:5$,其中较大的三角形一边上的中线长为$10\mathrm{cm}$,那么另一个三角形对应边上的中线长为
8
$\mathrm{cm}$。
答案:
8
6. 如图,在$\triangle ABC$中,点$E在AD$上,且点$E是\triangle ABC$的重心,若$S_{\triangle ABC} = 36$,则$S_{\triangle ACD}$等于
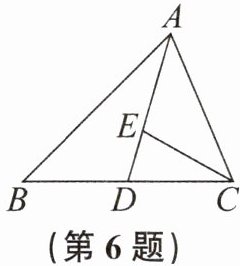
18
,$S_{\triangle DEC}$等于6
。
答案:
18 6
7. 求证:相似三角形对应边上的中线之比等于相似比。
要求:
(1)根据给出的$\triangle ABC及线段A'B'$,$\angle A'$($\angle A' = \angle A$),以线段$A'B'$为一边,在给出的图形上用尺规作出$\triangle A'B'C'$,使得$\triangle A'B'C' \backsim \triangle ABC$(不写作法,保留作图痕迹)。
(2)在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程。
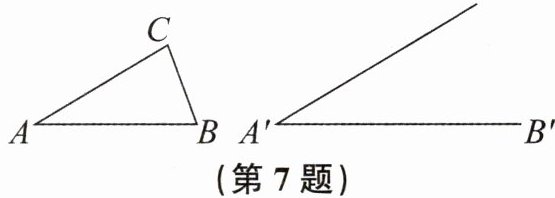
要求:
(1)根据给出的$\triangle ABC及线段A'B'$,$\angle A'$($\angle A' = \angle A$),以线段$A'B'$为一边,在给出的图形上用尺规作出$\triangle A'B'C'$,使得$\triangle A'B'C' \backsim \triangle ABC$(不写作法,保留作图痕迹)。
(2)在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程。

答案:
【解析】:
(1) 以$A'$为顶点,$A'B'$为一边,作$\angle A'B'C'=\angle B$,$B'C'$与$\angle A'$的另一边相交于$C'$,则$\triangle A'B'C'\backsim\triangle ABC$(尺规作图原理:两角分别相等的两个三角形相似)。
(2) 已知:$\triangle ABC\backsim\triangle A'B'C'$,$\frac{AB}{A'B'}=k$(相似比),$AD$是$\triangle ABC$中$BC$边上的中线,$A'D'$是$\triangle A'B'C'$中$B'C'$边上的中线。
求证:$\frac{AD}{A'D'}=k$。
证明:因为$\triangle ABC\backsim\triangle A'B'C'$,所以$\angle B = \angle B'$,$\frac{AB}{A'B'}=\frac{BC}{B'C'}$。
又因为$AD$、$A'D'$分别是$BC$、$B'C'$边上的中线,所以$BD=\frac{1}{2}BC$,$B'D'=\frac{1}{2}B'C'$,则$\frac{BD}{B'D'}=\frac{BC}{B'C'}$。
在$\triangle ABD$和$\triangle A'B'D'$中,$\left\{\begin{array}{l}\angle B = \angle B'\\frac{AB}{A'B'}=\frac{BD}{B'D'}\end{array}\right.$,根据两边成比例且夹角相等的两个三角形相似,可得$\triangle ABD\backsim\triangle A'B'D'$。
所以$\frac{AD}{A'D'}=\frac{AB}{A'B'}=k$。
【答案】:
(1) 以$A'$为顶点,$A'B'$为一边,作$\angle A'B'C'=\angle B$,$B'C'$与$\angle A'$的另一边相交于$C'$(作图痕迹略)。
(2) 已知:$\triangle ABC\backsim\triangle A'B'C'$,$\frac{AB}{A'B'}=k$,$AD$是$\triangle ABC$中$BC$边上的中线,$A'D'$是$\triangle A'B'C'$中$B'C'$边上的中线。
求证:$\frac{AD}{A'D'}=k$。
证明:因为$\triangle ABC\backsim\triangle A'B'C'$,所以$\angle B = \angle B'$,$\frac{AB}{A'B'}=\frac{BC}{B'C'}$。
又$BD=\frac{1}{2}BC$,$B'D'=\frac{1}{2}B'C'$,所以$\frac{BD}{B'D'}=\frac{BC}{B'C'}$,则$\frac{AB}{A'B'}=\frac{BD}{B'D'}$。
在$\triangle ABD$和$\triangle A'B'D'$中,$\left\{\begin{array}{l}\angle B = \angle B'\\frac{AB}{A'B'}=\frac{BD}{B'D'}\end{array}\right.$,所以$\triangle ABD\backsim\triangle A'B'D'$,所以$\frac{AD}{A'D'}=\frac{AB}{A'B'}=k$。
(1) 以$A'$为顶点,$A'B'$为一边,作$\angle A'B'C'=\angle B$,$B'C'$与$\angle A'$的另一边相交于$C'$,则$\triangle A'B'C'\backsim\triangle ABC$(尺规作图原理:两角分别相等的两个三角形相似)。
(2) 已知:$\triangle ABC\backsim\triangle A'B'C'$,$\frac{AB}{A'B'}=k$(相似比),$AD$是$\triangle ABC$中$BC$边上的中线,$A'D'$是$\triangle A'B'C'$中$B'C'$边上的中线。
求证:$\frac{AD}{A'D'}=k$。
证明:因为$\triangle ABC\backsim\triangle A'B'C'$,所以$\angle B = \angle B'$,$\frac{AB}{A'B'}=\frac{BC}{B'C'}$。
又因为$AD$、$A'D'$分别是$BC$、$B'C'$边上的中线,所以$BD=\frac{1}{2}BC$,$B'D'=\frac{1}{2}B'C'$,则$\frac{BD}{B'D'}=\frac{BC}{B'C'}$。
在$\triangle ABD$和$\triangle A'B'D'$中,$\left\{\begin{array}{l}\angle B = \angle B'\\frac{AB}{A'B'}=\frac{BD}{B'D'}\end{array}\right.$,根据两边成比例且夹角相等的两个三角形相似,可得$\triangle ABD\backsim\triangle A'B'D'$。
所以$\frac{AD}{A'D'}=\frac{AB}{A'B'}=k$。
【答案】:
(1) 以$A'$为顶点,$A'B'$为一边,作$\angle A'B'C'=\angle B$,$B'C'$与$\angle A'$的另一边相交于$C'$(作图痕迹略)。
(2) 已知:$\triangle ABC\backsim\triangle A'B'C'$,$\frac{AB}{A'B'}=k$,$AD$是$\triangle ABC$中$BC$边上的中线,$A'D'$是$\triangle A'B'C'$中$B'C'$边上的中线。
求证:$\frac{AD}{A'D'}=k$。
证明:因为$\triangle ABC\backsim\triangle A'B'C'$,所以$\angle B = \angle B'$,$\frac{AB}{A'B'}=\frac{BC}{B'C'}$。
又$BD=\frac{1}{2}BC$,$B'D'=\frac{1}{2}B'C'$,所以$\frac{BD}{B'D'}=\frac{BC}{B'C'}$,则$\frac{AB}{A'B'}=\frac{BD}{B'D'}$。
在$\triangle ABD$和$\triangle A'B'D'$中,$\left\{\begin{array}{l}\angle B = \angle B'\\frac{AB}{A'B'}=\frac{BD}{B'D'}\end{array}\right.$,所以$\triangle ABD\backsim\triangle A'B'D'$,所以$\frac{AD}{A'D'}=\frac{AB}{A'B'}=k$。
8. 如图,在$\mathrm{Rt}\triangle ABC$中,$\angle ACB = 90^{\circ}$,$G是\triangle ABC$的重心,连结$CG$,过点$G的直线MN // AB$,分别交$AC$,$BC于点M$,$N$。若$AB = 8$,求:
(1)线段$CG$的长。
(2)$CN与CB$的比。
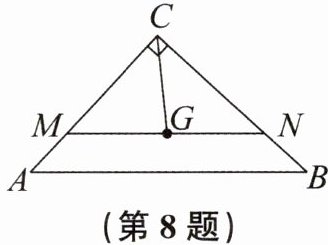
(1)线段$CG$的长。
(2)$CN与CB$的比。

答案:
(1)$\frac{8}{3}$.
(2)$2:3$.
(1)$\frac{8}{3}$.
(2)$2:3$.
查看更多完整答案,请扫码查看


