《2025年奔跑吧少年九年级数学全一册浙教版》

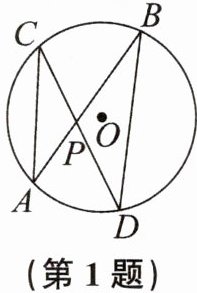
1. 如图,在$\odot O$中,弦$AB$,$CD相交于点P$。若$∠A= 42^{\circ }$,则$∠D$的度数为(B)

A. $43^{\circ }$
B. $42^{\circ }$
C. $84^{\circ }$
D. $21^{\circ }$

答案： B

2. 下列命题中,属于假命题的是(A)
A. 相等的圆周角所对的弧相等
B. 等弧所对的圆心角相等
C. 一条弧所对的圆周角等于它所对的圆心角的一半
D. 直径所对的圆周角为$90^{\circ }$

答案： A

3. 如图,$BD是\odot O$的直径,点$A$,$C在\odot O$上,$\overset{\frown }{AB}= \overset{\frown }{BC}$,$∠AOB= 60^{\circ }$,则$∠BDC$的度数为(D)
A. $60^{\circ }$
B. $45^{\circ }$
C. $35^{\circ }$
D. $30^{\circ }$

答案： D

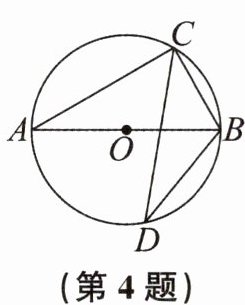
4. 如图,$AB是\odot O$的直径,点$C$,$D在\odot O$上。若$∠ABC= 60^{\circ }$,则$∠D$的度数为(B)

A. $25^{\circ }$
B. $30^{\circ }$
C. $35^{\circ }$
D. $40^{\circ }$

答案： B

5. 如图,在$\odot O$中,$OC⊥AB$,$∠APC= 32^{\circ }$,则$∠BOC$的度数为(D)
A. $16^{\circ }$
B. $32^{\circ }$
C. $58^{\circ }$
D. $64^{\circ }$

答案： D

6. 如图,在$\odot O$中,$\overset{\frown }{AB}= \overset{\frown }{AC}$,$∠ABC= 80^{\circ }$,则$∠BOC$的度数为$ 40^{\circ} $。

答案： $ 40^{\circ} $

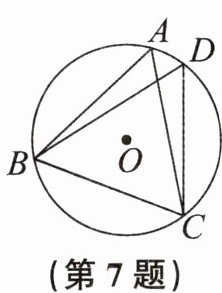
7. 如图,$AC$,$BD是\odot O$的两条相交弦,$∠ACB= ∠CDB$,$AB= 2$,则$BC$的长为2。

答案： 2

8. 如图,$AB是\odot O$的直径,点$C$,$D$,$E在\odot O$上。若$∠AED= 20^{\circ }$,则$∠BCD$的度数为$ 110^{\circ} $。

答案： $ 110^{\circ} $

9. 如图,点$A$,$B$,$C$,$D在\odot O$上,且$AC// BD$,延长$AB$,$CD相交于点P$。求证：$PA= PC$。

答案： 【解析】：
- 因为$AC// BD$，根据两直线平行，内错角相等，所以$\angle ABD=\angle A$。
- 又因为$\angle ABD$和$\angle C$是同弧所对的圆周角，根据同弧所对的圆周角相等，所以$\angle ABD = \angle C$。
- 由上述两个结论可得$\angle A=\angle C$。
- 在$\triangle PAC$中，根据等角对等边，所以$PA = PC$。
【答案】：
因为$AC// BD$，所以$\angle ABD=\angle A$（两直线平行，内错角相等）。
因为$\angle ABD=\angle C$（同弧所对的圆周角相等），所以$\angle A = \angle C$。
在$\triangle PAC$中，$\angle A=\angle C$，所以$PA = PC$（等角对等边）。
故$PA = PC$得证。

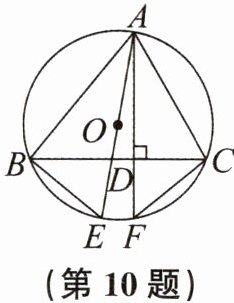
10. 如图,$AB$,$AC是\odot O$的弦,$AD⊥BC于点D$,交$\odot O于点F$,$AE是\odot O$的直径。求证：$\overset{\frown }{BE}= \overset{\frown }{CF}$。

答案： 【解析】：
连接$BE$，因为$AE$是$\odot O$的直径，所以$\angle ABE = 90^{\circ}$（直径所对的圆周角是直角）。
又因为$AD\perp BC$，所以$\angle ADC = 90^{\circ}$。
$\angle AEB$和$\angle ACB$所对的弧都是$\overset{\frown }{AB}$，根据同弧所对的圆周角相等，可得$\angle AEB=\angle ACB$。
在$\triangle ABE$和$\triangle ADC$中，$\angle ABE=\angle ADC = 90^{\circ}$，$\angle AEB=\angle ACB$，所以$\angle BAE=\angle CAD$（三角形内角和为$180^{\circ}$）。
根据在同圆或等圆中，相等的圆周角所对的弧相等，因为$\angle BAE$所对的弧是$\overset{\frown }{BE}$，$\angle CAD$所对的弧是$\overset{\frown }{CF}$，所以$\overset{\frown }{BE}=\overset{\frown }{CF}$。
【答案】：
连接$BE$，
$\because AE$是$\odot O$直径，$\therefore\angle ABE = 90^{\circ}$（直径所对圆周角是直角），
$\because AD\perp BC$，$\therefore\angle ADC = 90^{\circ}$，
$\because\angle AEB$与$\angle ACB$是$\overset{\frown }{AB}$所对圆周角 ，$\therefore\angle AEB=\angle ACB$，
在$\triangle ABE$和$\triangle ADC$中，$\angle ABE=\angle ADC$，$\angle AEB=\angle ACB$，
$\therefore\angle BAE=\angle CAD$（三角形内角和$180^{\circ}$），
$\therefore\overset{\frown }{BE}=\overset{\frown }{CF}$（同圆或等圆中，相等圆周角所对弧相等）。
故$\overset{\frown }{BE}=\overset{\frown }{CF}$得证。