2025年奔跑吧少年九年级数学全一册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年九年级数学全一册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 抛物线$y= x^{2}+4x+4$与x轴的交点个数为(
A. 0
B. 1
C. 2
D. 3
B
)A. 0
B. 1
C. 2
D. 3
答案:
B
2. 已知二次函数$y= ax^{2}+bx+c$的变量x,y的部分对应值如下表所示,根据表中信息,可得一元二次方程$ax^{2}+bx+c= 0的一个解x_{1}$的范围是(
|x|…|-3|-2|-1|0|1|…|
|y|…|-11|-5|-1|1|1|…|
A. $-3<x_{1}<-2$
B. $-2<x_{1}<-1$
C. $-1<x_{1}<0$
D. $0<x_{1}<1$
C
)|x|…|-3|-2|-1|0|1|…|
|y|…|-11|-5|-1|1|1|…|
A. $-3<x_{1}<-2$
B. $-2<x_{1}<-1$
C. $-1<x_{1}<0$
D. $0<x_{1}<1$
答案:
C
3. 如图,点$A(2.18,-0.71)$,$B(2.68,0.54)在二次函数y= ax^{2}+bx+c(a≠0)$的图象上,则方程$ax^{2}+bx+c= 0$的一个近似值可能是(

A. 2.18
B. 2.68
C. 2.84
D. 2.45
D
)
A. 2.18
B. 2.68
C. 2.84
D. 2.45
答案:
D
4. 如图所示为二次函数$y= -x^{2}+2x+4$的图象,使$y≥1$成立的x的取值范围是(
A. $-1≤x≤3$
B. $x≤-1$
C. $x≥1$
D. $x≤-1或x≥3$
A
)A. $-1≤x≤3$
B. $x≤-1$
C. $x≥1$
D. $x≤-1或x≥3$
答案:
A
5. 已知关于x的一元二次方程$x^{2}-bx+c= 0的解为x_{1}= -1$,$x_{2}= 3$,则二次函数$y= x^{2}-bx+c$的对称轴是(
A. 直线$x= -1$
B. 直线$x= 0$
C. 直线$x= 1$
D. 直线$x= 2$
C
)A. 直线$x= -1$
B. 直线$x= 0$
C. 直线$x= 1$
D. 直线$x= 2$
答案:
C
6. 已知函数$y= 2x^{2}+3x+k$的图象与x轴有交点,则k的取值范围是
$ k \leq \frac{9}{8} $
。
答案:
$ k \leq \frac{9}{8} $
7. 一个小球从地面竖直向上弹出,它在空中距离地面的高度$h(m)与弹出的时间t(s)满足的关系式为h= 15t-5t^{2}$。当小球第一次距离地面10m时,小球弹出的时间为
1
s。
答案:
1
8. 已知二次函数$y= -x^{2}-2x+2$。
(1)填写表,并在给出的平面直角坐标系中画出这个二次函数的图象。
|x|…|-3|-2|-1|0|1|…|
|y|…|
(2)结合函数图象,请直接写出方程$-x^{2}-2x+2= 0$的近似解(精确到0.1)。
(1)填写表,并在给出的平面直角坐标系中画出这个二次函数的图象。
|x|…|-3|-2|-1|0|1|…|
|y|…|
-1
|2
|3
|2
|-1
|…|(2)结合函数图象,请直接写出方程$-x^{2}-2x+2= 0$的近似解(精确到0.1)。
$x_{1}\approx - 2.7$,$x_{2}\approx0.7$

答案:
1. (1)
当$x = - 3$时:
把$x=-3$代入$y=-x^{2}-2x + 2$,根据$y=-(-3)^{2}-2×(-3)+2$,先算乘方$(-3)^{2}=9$,则$y=-9 + 6+2=-1$。
当$x=-2$时:
把$x = - 2$代入$y=-x^{2}-2x + 2$,$y=-(-2)^{2}-2×(-2)+2$,先算乘方$(-2)^{2}=4$,则$y=-4 + 4+2=2$。
当$x=-1$时:
把$x=-1$代入$y=-x^{2}-2x + 2$,$y=-(-1)^{2}-2×(-1)+2$,先算乘方$(-1)^{2}=1$,则$y=-1 + 2+2=3$。
当$x = 0$时:
把$x = 0$代入$y=-x^{2}-2x + 2$,$y=-0^{2}-2×0+2=2$。
当$x = 1$时:
把$x = 1$代入$y=-x^{2}-2x + 2$,$y=-1^{2}-2×1+2$,先算乘方$1^{2}=1$,则$y=-1-2 + 2=-1$。
表格为:
| $x$ |…| $-3$ | $-2$ | $-1$ | $0$ | $1$ |…|
| $y$ |…| $-1$ | $2$ | $3$ | $2$ | $-1$ |…|
画图象:对于二次函数$y=-x^{2}-2x + 2$,其对称轴为$x=-\frac{b}{2a}$,其中$a=-1$,$b=-2$,则$x=-\frac{-2}{2×(-1)}=-1$,顶点坐标为$(-1,3)$,再根据表格中的点$(-3,-1)$,$(-2,2)$,$(0,2)$,$(1,-1)$等,用平滑曲线连接这些点画出图象。
2. (2)
方程$-x^{2}-2x + 2 = 0$的解就是二次函数$y=-x^{2}-2x + 2$与$x$轴交点的横坐标。
观察图象,当$y = 0$时,$x\approx - 2.7$或$x\approx0.7$。
所以(1)表格已填好;(2)方程$-x^{2}-2x + 2 = 0$的近似解为$x_{1}\approx - 2.7$,$x_{2}\approx0.7$。
当$x = - 3$时:
把$x=-3$代入$y=-x^{2}-2x + 2$,根据$y=-(-3)^{2}-2×(-3)+2$,先算乘方$(-3)^{2}=9$,则$y=-9 + 6+2=-1$。
当$x=-2$时:
把$x = - 2$代入$y=-x^{2}-2x + 2$,$y=-(-2)^{2}-2×(-2)+2$,先算乘方$(-2)^{2}=4$,则$y=-4 + 4+2=2$。
当$x=-1$时:
把$x=-1$代入$y=-x^{2}-2x + 2$,$y=-(-1)^{2}-2×(-1)+2$,先算乘方$(-1)^{2}=1$,则$y=-1 + 2+2=3$。
当$x = 0$时:
把$x = 0$代入$y=-x^{2}-2x + 2$,$y=-0^{2}-2×0+2=2$。
当$x = 1$时:
把$x = 1$代入$y=-x^{2}-2x + 2$,$y=-1^{2}-2×1+2$,先算乘方$1^{2}=1$,则$y=-1-2 + 2=-1$。
表格为:
| $x$ |…| $-3$ | $-2$ | $-1$ | $0$ | $1$ |…|
| $y$ |…| $-1$ | $2$ | $3$ | $2$ | $-1$ |…|
画图象:对于二次函数$y=-x^{2}-2x + 2$,其对称轴为$x=-\frac{b}{2a}$,其中$a=-1$,$b=-2$,则$x=-\frac{-2}{2×(-1)}=-1$,顶点坐标为$(-1,3)$,再根据表格中的点$(-3,-1)$,$(-2,2)$,$(0,2)$,$(1,-1)$等,用平滑曲线连接这些点画出图象。
2. (2)
方程$-x^{2}-2x + 2 = 0$的解就是二次函数$y=-x^{2}-2x + 2$与$x$轴交点的横坐标。
观察图象,当$y = 0$时,$x\approx - 2.7$或$x\approx0.7$。
所以(1)表格已填好;(2)方程$-x^{2}-2x + 2 = 0$的近似解为$x_{1}\approx - 2.7$,$x_{2}\approx0.7$。
9. 二次函数$y= ax^{2}+bx+c(a≠0)$的图象如图所示,根据图象解答下列问题:
(1)求二次函数的表达式。
(2)关于x的方程$ax^{2}+bx+c= 0$的根是______
(3)请直接写出关于x的不等式$ax^{2}+bx+c>0$的解:______
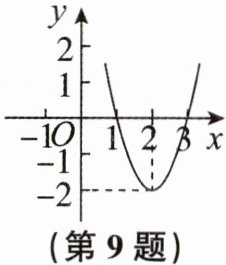
(1)
(1)求二次函数的表达式。
(2)关于x的方程$ax^{2}+bx+c= 0$的根是______
$ x_{1} = 1 $, $ x_{2} = 3 $
。(3)请直接写出关于x的不等式$ax^{2}+bx+c>0$的解:______
$ x < 1 $或$ x > 3 $
。
(1)
$ y = 2x^{2} - 8x + 6 $
答案:
(1)$ y = 2x^{2} - 8x + 6 $.
(2)$ x_{1} = 1 $, $ x_{2} = 3 $
(3)$ x < 1 $或$ x > 3 $
(1)$ y = 2x^{2} - 8x + 6 $.
(2)$ x_{1} = 1 $, $ x_{2} = 3 $
(3)$ x < 1 $或$ x > 3 $
查看更多完整答案,请扫码查看


