2025年奔跑吧少年九年级数学全一册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年九年级数学全一册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 若扇形的圆心角为$90^{\circ }$,半径为6,则该扇形的弧长为(
A. $\frac {2}{3}π$
B. $2π$
C. $3π$
D. $6π$
C
)A. $\frac {2}{3}π$
B. $2π$
C. $3π$
D. $6π$
答案:
C
2. 如果一个扇形的弧长是$\frac {4}{3}π$,半径是6,那么此扇形的圆心角的度数为(
A. $40^{\circ }$
B. $45^{\circ }$
C. $60^{\circ }$
D. $80^{\circ }$
A
)A. $40^{\circ }$
B. $45^{\circ }$
C. $60^{\circ }$
D. $80^{\circ }$
答案:
A
3. 如图,在$5×5$的正方形网格中,每个小正方形的边长都为1,若将$△AOB$绕点O按顺时针方向旋转$90^{\circ }得到△A'OB'$,则点A运动的路径$\widehat {AA'}$的长为(
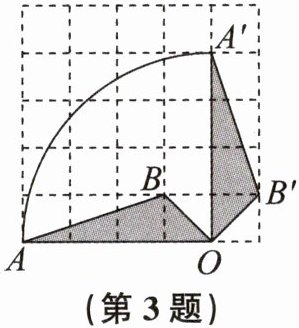
A. $π$
B. $2π$
C. $4π$
D. $8π$
B
) 
A. $π$
B. $2π$
C. $4π$
D. $8π$
答案:
B
4. 如图所示为两个同心圆的一部分,已知$OB= \frac {1}{2}OA$,则$\widehat {BC}的长是\widehat {AD}$长的(
A. $\frac {1}{2}$
B. 2倍
C. $\frac {1}{4}$
D. 4倍
A
)A. $\frac {1}{2}$
B. 2倍
C. $\frac {1}{4}$
D. 4倍
答案:
A
5. 如图,分别以$△ABC$的三个顶点为圆心,作半径均为1的三个圆,三圆两两不相交,那么三个圆落在$△ABC$内的三段弧的长度之和为(
A. $3π$
B. $2π$
C. $π$
D. $\frac {1}{2}π$
C
)A. $3π$
B. $2π$
C. $π$
D. $\frac {1}{2}π$
答案:
C
6. 如图,已知扇形AOB的圆心角的度数为$60^{\circ }$,$\widehat {AB}的长为2π$,则该扇形的直径为
12
.
答案:
12
7. 如图,已知正方形的边长为2 cm,以对角的两个顶点为圆心,2 cm长为半径画弧,则所得到的两条弧的长度之和为
$2\pi$
cm.
答案:
$ 2\pi $
8. 一个滑轮起重装置如图所示,滑轮的半径是10 cm,OA是滑轮的一条半径,当OA绕轴心O按逆时针方向旋转$108^{\circ }$时,重物上升的高度为
$6\pi$
cm.
答案:
$ 6\pi $
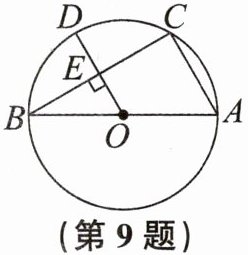
9. 如图,已知AB是$\odot O$的直径,C是$\odot O$上一点,连结BC,AC,$∠A= 60^{\circ }$,半径$OD⊥BC$,垂足为E.
(1)求$∠BOD$的度数.
(2)若$AB= 8$,求$\widehat {BD}$的长.
(1)求$∠BOD$的度数.
(2)若$AB= 8$,求$\widehat {BD}$的长.

答案:
(1) $ 60^{\circ} $.
(2) $ \frac{4}{3}\pi $.
(1) $ 60^{\circ} $.
(2) $ \frac{4}{3}\pi $.
10. 有一段圆弧形的公路弯道,其所对的圆心角的度数是$150^{\circ }$,半径是400 m,一辆汽车以40 km/h的速度开过这段弯道,需要多少分钟?
答案:
$ \frac{\pi}{2} $ min.
查看更多完整答案,请扫码查看


