2025年奔跑吧少年九年级数学全一册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年九年级数学全一册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
11. 如图,$P是线段AB$的黄金分割点,且$PA > PB$,若$S_{1}表示以PA$为一边的正方形的面积,$S_{2}表示长为AB$、宽为$PB$的矩形的面积,则$S_{1}与S_{2}$的大小关系是(
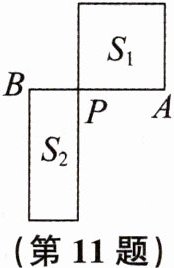
A. $S_{1} > S_{2}$
B. $S_{1} = S_{2}$
C. $S_{1} < S_{2}$
D. 无法确定
B
)
A. $S_{1} > S_{2}$
B. $S_{1} = S_{2}$
C. $S_{1} < S_{2}$
D. 无法确定
答案:
B
12. 如图,已知线段$AB$,按以下步骤作图:①过点$B作BC\perp AB$,使$BC = \frac{1}{2}AB$,连结$AC$;②以点$C$为圆心,$BC$长为半径画弧,交$AC于点D$;③以点$A$为圆心,$AD$长为半径画弧,交$AB于点E$. 若$AE = mAB$,则$m$的值为
$ \frac { \sqrt { 5 } - 1 } { 2 } $
.
答案:
$ \frac { \sqrt { 5 } - 1 } { 2 } $
13. 如图,在$\triangle ABC$中,$CD\perp AB于点D$,$AD = 8cm$,$BD = 3cm$,且$CD是AD与BD$的比例中项,求$\triangle ABC$的面积.
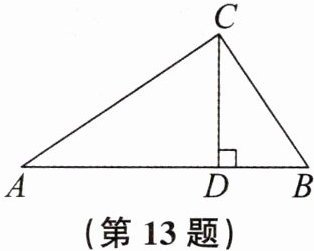

答案:
$ 11 \sqrt { 6 } \mathrm { cm } ^ { 2 } $.
14. 我们把有一个内角为$36^{\circ}$的等腰三角形称为“黄金三角形”(底边长与腰长的比值或腰长与底边长的比值为黄金比). 如图,已知$\triangle ABC$,$\triangle BDC$,$\triangle DEC都是顶角为36^{\circ}$的“黄金三角形”,$AB = 1$,求$DE$的长.
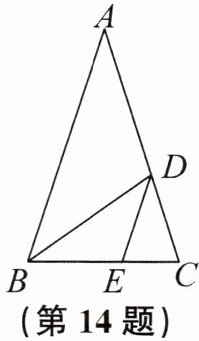

答案:
$ \frac { 3 - \sqrt { 5 } } { 2 } $.
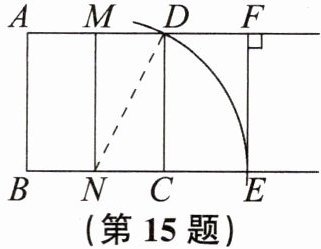
15. 宽与长的比是$\frac{\sqrt{5} - 1}{2}$的矩形叫“黄金矩形”. 心理测试表明:“黄金矩形”令人赏心悦目,它给我们以协调、匀称的美感. 现将小波同学在数学活动课中所作“黄金矩形”的方法归纳如下(如图):
第一步:作一个正方形$ABCD$.
第二步:分别取$AD$,$BC的中点M$,$N$,连结$MN$.
第三步:以点$N$为圆心,$ND$长为半径画弧,交$BC的延长线于点E$.
第四步:过点$E作EF\perp AD$,交$AD的延长线于点F$.
请你根据以上作法,证明矩形$DCEF$为“黄金矩形”.
第一步:作一个正方形$ABCD$.
第二步:分别取$AD$,$BC的中点M$,$N$,连结$MN$.
第三步:以点$N$为圆心,$ND$长为半径画弧,交$BC的延长线于点E$.
第四步:过点$E作EF\perp AD$,交$AD的延长线于点F$.
请你根据以上作法,证明矩形$DCEF$为“黄金矩形”.

答案:
【解析】:
设正方形$ABCD$的边长为$2a$。
因为$N$为$BC$中点,$BC = 2a$,所以$NC=\frac{1}{2}BC = a$。
在$Rt\triangle DNC$中,根据勾股定理$DN=\sqrt{NC^{2}+DC^{2}}$,已知$DC = 2a$,$NC = a$,则$DN=\sqrt{a^{2}+(2a)^{2}}=\sqrt{5}a$。
又因为$NE = ND$,所以$CE=NE - NC=\sqrt{5}a - a=(\sqrt{5}-1)a$。
而$DC = 2a$,那么$\frac{CE}{DC}=\frac{(\sqrt{5}-1)a}{2a}=\frac{\sqrt{5}-1}{2}$。
因为矩形$DCEF$中$\angle DCE = 90^{\circ}$,$EF\perp AD$,$AD// BC$,所以矩形$DCEF$的宽$CE$与长$DC$的比是$\frac{\sqrt{5}-1}{2}$。
【答案】:
设正方形$ABCD$边长为$2a$,由$N$为$BC$中点得$NC = a$,在$Rt\triangle DNC$中,$DN=\sqrt{NC^{2}+DC^{2}}=\sqrt{a^{2}+(2a)^{2}}=\sqrt{5}a$,因为$NE = ND$,所以$CE = (\sqrt{5}-1)a$,则$\frac{CE}{DC}=\frac{(\sqrt{5}-1)a}{2a}=\frac{\sqrt{5}-1}{2}$,所以矩形$DCEF$为“黄金矩形”。
设正方形$ABCD$的边长为$2a$。
因为$N$为$BC$中点,$BC = 2a$,所以$NC=\frac{1}{2}BC = a$。
在$Rt\triangle DNC$中,根据勾股定理$DN=\sqrt{NC^{2}+DC^{2}}$,已知$DC = 2a$,$NC = a$,则$DN=\sqrt{a^{2}+(2a)^{2}}=\sqrt{5}a$。
又因为$NE = ND$,所以$CE=NE - NC=\sqrt{5}a - a=(\sqrt{5}-1)a$。
而$DC = 2a$,那么$\frac{CE}{DC}=\frac{(\sqrt{5}-1)a}{2a}=\frac{\sqrt{5}-1}{2}$。
因为矩形$DCEF$中$\angle DCE = 90^{\circ}$,$EF\perp AD$,$AD// BC$,所以矩形$DCEF$的宽$CE$与长$DC$的比是$\frac{\sqrt{5}-1}{2}$。
【答案】:
设正方形$ABCD$边长为$2a$,由$N$为$BC$中点得$NC = a$,在$Rt\triangle DNC$中,$DN=\sqrt{NC^{2}+DC^{2}}=\sqrt{a^{2}+(2a)^{2}}=\sqrt{5}a$,因为$NE = ND$,所以$CE = (\sqrt{5}-1)a$,则$\frac{CE}{DC}=\frac{(\sqrt{5}-1)a}{2a}=\frac{\sqrt{5}-1}{2}$,所以矩形$DCEF$为“黄金矩形”。
查看更多完整答案,请扫码查看


