《2025年奔跑吧少年九年级数学全一册浙教版》

如图,已知直线$l_{1},l_{2},l_{3}分别交直线l_{4}于点A,B,C$,交直线$l_{5}于点D,E,F$,且$l_{1}// l_{2}// l_{3}$.若$AB= 4$,$AC= 6$,$DF= 9$,则$EF$的长为(A)
A. 3
B. 6
C. 4
D. 5

答案： A

互动题1-1 若$\frac {m}{n}= \frac {2}{3}$,则$\frac {2m}{m+n}$的值为(B)
A. $\frac {10}{3}$
B. $\frac {4}{5}$
C. $\frac {6}{5}$
D. $\frac {5}{4}$

答案： B

互动题1-2 小慧同学在学习了九年级上册“4.1比例线段”后,发现学习内容是一个逐步特殊

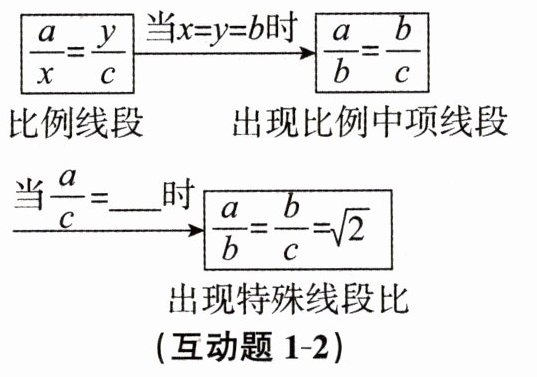
化的过程,请在横线上填写适当的数值,感受这种特殊化的学习过程.图中横线处应填:2.

答案： 2

互动题1-3 如图,乐器上的一根弦$AB$的长为18cm,两个端点$A,B$固定在乐器板面上,支撑点$C是弦AB靠近点B$的黄金分割点,则线段$AC$的长为$(9\sqrt {5}-9)$$cm$.

答案： $(9\sqrt {5}-9)$

典例2 如图,已知$\frac {AB}{DB}= \frac {BC}{BE}= \frac {AC}{DE}$,求证:$\triangle ABD\backsim \triangle CBE$.

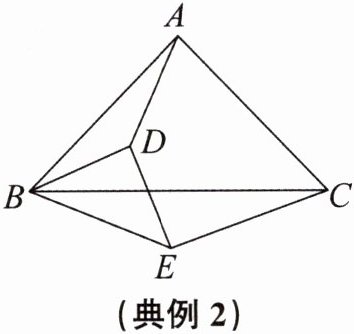
答案： 【解析】：
已知$\frac{AB}{DB}=\frac{BC}{BE}=\frac{AC}{DE}$，根据“三边成比例的两个三角形相似”，可得$\triangle ABC\backsim\triangle DBE$。
所以$\angle ABC = \angle DBE$，则$\angle ABC - \angle DBC = \angle DBE - \angle DBC$，即$\angle ABD = \angle CBE$。
又因为$\frac{AB}{DB}=\frac{BC}{BE}$，根据“两边成比例且夹角相等的两个三角形相似”，可得$\triangle ABD\backsim\triangle CBE$。
【答案】：
因为$\frac{AB}{DB}=\frac{BC}{BE}=\frac{AC}{DE}$，所以$\triangle ABC\backsim\triangle DBE$，所以$\angle ABC = \angle DBE$，进而$\angle ABD = \angle CBE$。又$\frac{AB}{DB}=\frac{BC}{BE}$，所以$\triangle ABD\backsim\triangle CBE$。

互动题2-1 如图,在四边形$ABCD$中,已知$∠ADC= ∠BAC$,则下列条件中,补充后不能判定$\triangle ADC和\triangle BAC$相似的是(C)
A. $CA平分∠BCD$
B. $∠DAC= ∠B$
C. $AC^{2}= BC\cdot CD$
D. $\frac {AD}{AB}= \frac {DC}{AC}$

答案： C

互动题2-2 如图,四个三角形的顶点都在方格子的格点上,下列选项中,两个三角形相似的是( )


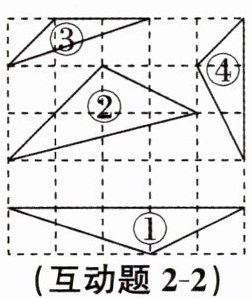
A. ①④
B. ①③
C. ②③
D. ②④

答案： B

互动题2-3 如图,在$\triangle ABC$中,$AB= AC$,$∠A= 36^{\circ }$,$BD平分∠ABC$,$DE// BC$,在图中与$\triangle ABC$相似的三角形的个数为2.

答案： 2