《2025年从课本到奥数同步练五年级数学下册苏教版》

1. 选择题。
(1) 圆周长是$2\pi r$，半圆的周长是(　　　)。
A. $\pi r$　　　B. $\pi r + r$　　C. $\pi r + 2r$

答案：
(1)C　

(2) 大小不同的两个圆半径各增加10厘米，两个圆增加的周长相比，(　　　)多。
A. 大圆　　B. 小圆　　　C. 同样

答案：
(2)C　

(3) 如图，从A地到B地有甲、乙两条路可以走，这两条路的长度相比较，(　　　)。
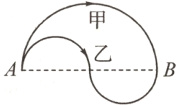
A. 同样长　B. 甲长　　　C. 乙长

答案：
(3)A　[提示:可以设小圆直径为1。]

2. 仓库里有一个油桶，油桶底面是半径为0.2米的圆，从一面墙滚到另一面墙，正好滚了5圈。这两面墙之间的距离是多少米？

答案： π×(0.2×2)×5 = 2π(米) 2π + 0.2 + 0.2=(2π + 0.4)米(或6.68米)　[提示:滚动5圈是5个周长,但两墙之间的距离除了5个周长还有一头一尾的2个半径。]

3. 一个量角器的周长是25.7厘米，它的半径是多少厘米? ($\pi$取3.14)

答案： 解:设它的半径是x厘米。2×3.14×x÷2 + 2x = 25.7 3.14x + 2x = 25.7 5.14x = 25.7 x = 25.7÷5.14 x = 5　[提示:注意半圆的周长 = 圆周长的一半 + 一条直径的长。]

4. 明明把一张圆纸片连续对折两次，得到一个扇形，测量出这个扇形的圆弧长度是4.71厘米。这个扇形的周长是多少厘米?

答案： 4.71×4 = 18.84(厘米) 18.84÷3.14÷2 = 3(厘米) 4.71 + 3 + 3 = 10.71(厘米)　[提示:根据扇形圆弧长4.71厘米是圆周长的$\frac{1}{4}$，可以求出圆周长。要求扇形的周长，用扇形圆弧长 + 2条半径的长。]

例 如图，用绳子将4罐可乐捆扎在一起，至少需要多少厘米的绳子? (已知每个可乐罐底面的直径是6厘米，打结处的长度为5厘米)($\pi$取3.14)

分析与解答 图中绳子有直的，也有弯的，直的部分就是圆的直径，弯的部分就是圆周长的四分之一(如图)，因此绳子的长度应等于四条直径的长度与一个圆的周长的和，再加上打结处的长度。
6×4 + 6×3.14 + 5 = 47.84(厘米)
答：至少需要47.84厘米的绳子。
小窍门 计算组合图形的周长，可以分析图形的组成，将直线与曲线部分的长度分别计算，有些曲线可以合并成完整的圆，合并计算。

答案：

1. 如图，将2个底面直径是8厘米的酒瓶并排捆扎在一起，至少需要多长的绳子? (接头处忽略不计)

答案： π×8 + 8×2=(8π + 16)厘米(或41.12厘米)
[提示:曲线部分的长度相当于一个圆的周长，直线部分就是两条直径的长度。]

2. 计算下图中阴影部分的周长。

答案： 8×4 + 8×π=(8π + 32)厘米(或57.12厘米)
[提示:图中有4个扇形，弧线可以合并成一个圆，再加上正方形的4条边长，即可算出阴影部分的周长。]

3. 计算下图中阴影部分的周长。

答案： π×8÷2 = 4π(厘米)(或12.56厘米)　[提示:图中有3个扇形，弧线的长度和就是阴影部分的周长，根据三角形内角和是180°，可知这3个扇形可以拼成一个圆心角为180°的扇形，即半圆。]