《2025年通成学典课时作业本高中数学选择性必修第三册人教版》

1.(2025·榆林期中)$10 × 9 × 8 × ·s × 5$可表示为 (B)

A.$\mathrm{A}_{10}^{5}$
B.$\mathrm{A}_{10}^{6}$
C.$\mathrm{A}_{11}^{5}$
D.$\mathrm{A}_{11}^{6}$

答案： 1.B

2. 下列各式中，不等于$n !(n \in \mathbf{N}^*)$的是(B)

A.$\mathrm{A}_{n-1}^{n-1}$
B.$\mathrm{A}_{n+1}^{n+1}$
C.$n \mathrm{A}_{n-1}^{n-1}$
D.$(n-m) !\mathrm{A}_{n}^{m}$

答案： 2.B

3.(2025·镇江期中)$\mathrm{A}_{2025}^{10}$等于 (B)

A.$2025 × 2024 × 2023 × ·s × 2015$
B.$2025 × 2024 × 2023 × ·s × 2016$
C.$\frac{2025!}{10!}$
D.$\frac{2025!}{2015! × 10!}$

答案： 3.B

4.(多选题)(2025·东莞段考)下列属于排列问题的是 (ACD)

A.从6人中选2人分别去游泳和跳绳
B.从班上30名男生中选出5人组成一个篮球队
C.从10个不同的质数中取2个数求其商
D.从5,6,7三个数中取2个数组成一个两位数

答案： 4.ACD

5.(多选题)下列等式中，成立的是 (ACD)

A.$\mathrm{A}_{n}^{3}=(n-2) \mathrm{A}_{n}^{2}$
B.$\frac{1}{n} \mathrm{A}_{n+1}^{n+1}=\mathrm{A}_{n+1}^{n+1}$
C.$n \mathrm{A}_{n-2}^{n-2}=\mathrm{A}_{n}^{n}$
D.$\frac{n}{n-m} \mathrm{A}_{n-1}^{m-1}=\mathrm{A}_{n}^{m}$

答案： 5.ACD

6. 若$\mathrm{A}_{m}^{5}=2 \mathrm{A}_{m}^{3}$，则$m=$5.

答案： 6.5

7. 如果$\mathrm{A}_{n}^{m}=17 × 16 × ·s × 5 × 4$，那么$n=$17，$m=$14.

答案： 7.17 14

8. 核心素养 数学运算 (1) 计算：$\mathrm{A}_{4}^{1}+\mathrm{A}_{4}^{2}+\mathrm{A}_{4}^{3}+\mathrm{A}_{4}^{4}$；
(2) 计算：$4 \mathrm{A}_{4}^{2}+5 \mathrm{A}_{5}^{3}$；
(3) 已知$\mathrm{A}_{n}^{2}=7 \mathrm{A}_{n-4}^{2}$，求$n$的值.

答案： 8.解：
(1)$A_{4}^{1}+A_{4}^{2}+A_{4}^{3}+A_{4}^{4}=4 + 4×3 + 4×3×2 + 4×3×2×1 = 64$。
(2)$4A_{4}^{2}+5A_{5}^{3}=4×4×3 + 5×5×4×3 = 348$。
(3)由$A_{n}^{2}=7A_{n - 4}^{2}$，得$n - 4\geqslant2,n\in N^{*}$，即$n\geqslant6$，$n\in N^{*}$，则$n(n - 1)=7(n - 4)(n - 5)$，整理，得$(3n - 10)(n - 7)=0$，所以$n = 7$。

9.(2024·云南段考)现有粉玫瑰、红玫瑰、香槟玫瑰、紫玫瑰、白玫瑰、蓝玫瑰各1枝，从中取5枝放入5根不同的玻璃管中，每根玻璃管放1枝，则不同的放置方法有 (D)

A.6种
B.120种
C.360种
D.720种

答案： 9.D

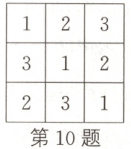
10. 将1,2,3填入$3 × 3$的方格中，要求每行、每列都没有重复数字. 如图所示为其中一种填法，则不同的填写方法共有 (B)



A.6种
B.12种
C.24种
D.48种

答案： 10.B