2025年通成学典课时作业本高中数学选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通成学典课时作业本高中数学选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. (2025·蚌埠阶段练习)若某地未来连续3 天每天下雨的概率均为$\frac{2}{3}$,则这3 天中只有
1天下雨的概率为
(
A.$\frac{2}{9}$
B.$\frac{4}{9}$
C.$\frac{2}{27}$
D.$\frac{4}{27}$
1天下雨的概率为
(
A
)A.$\frac{2}{9}$
B.$\frac{4}{9}$
C.$\frac{2}{27}$
D.$\frac{4}{27}$
答案:
1.A
2. 已知随机变量$X\sim B(2,p)$.若$P(X\geq1)=\frac{5}{9}$,则$p$的值为
(
A.$\frac{1}{3}$
B.$\frac{2}{3}$
C.$\frac{\sqrt{5}}{3}$
D.$\frac{4}{9}$
(
A
)A.$\frac{1}{3}$
B.$\frac{2}{3}$
C.$\frac{\sqrt{5}}{3}$
D.$\frac{4}{9}$
答案:
2.A
3. (多选题)(2025·浙江期中)已知随机变量$X\sim B\left(6,\frac{1}{3}\right)$,则下列说法正确的是
(
A.$P(X=2)=P(X=4)$
B.$E(3X+2)=8$
C.$D(X)=\frac{4}{3}$
D.$D(3X+2)=6$
(
BC
)A.$P(X=2)=P(X=4)$
B.$E(3X+2)=8$
C.$D(X)=\frac{4}{3}$
D.$D(3X+2)=6$
答案:
3.BC
4. 已知两个随机变量$X,Y$满足$X+Y=8$.如果$X\sim B\left(25,\frac{3}{5}\right)$,那么$E(Y+D(Y))=$
−1
.
答案:
4.−1
5. (2024·驻马店期末)如图,一质点在外力的作用下,从原点出发,每次向左移动的概率为$\frac{1}{3}$,向右移动的概率为$\frac{2}{3}$.若该质点每次移动一个单位长度,记经过$n$次$(n\in \mathbf{N})$移动后,该质点位于数$X$的位置.
(1)当$n=4$时,求$P(X=-2),P(X>0)$;
(2)当$n=5$时,求随机变量$X$的分布列及数
学期望.

(1)当$n=4$时,求$P(X=-2),P(X>0)$;
(2)当$n=5$时,求随机变量$X$的分布列及数
学期望.

答案:
5. 解:
(1) 当$n = 4$时,质点所能到达的数$X$必满足$\vert X\vert\leq4$且$X$为偶数.若$X = - 2$,则表示该质点向右移动$1$次,向左移动$3$次.所以$P(X = - 2) = C_{4}^{3}×(\frac{1}{3})^3×\frac{2}{3} = \frac{8}{81}$.所以$P(X > 0) = P(X = 2) + P(X = 4) = C_{4}^{1}×\frac{1}{3}×(\frac{2}{3})^3 + C_{4}^{0}×(\frac{2}{3})^4 = \frac{32}{81} + \frac{16}{81} = \frac{16}{27}$.
(2) 当$n = 5$时,质点所能到达的数$X$必满足$\vert X\vert\leq5$且$X$为奇数,所以随机变量$X$的所有可能取值为$- 5$,$- 3$,$- 1$,$1$,$3$,$5$.所以$P(X = - 5) = C_{5}^{5}×(\frac{1}{3})^5 = \frac{1}{243}$,$P(X = - 3) = C_{5}^{4}×(\frac{1}{3})^4×\frac{2}{3} = \frac{10}{243}$,$P(X = - 1) = C_{5}^{3}×(\frac{1}{3})^3×(\frac{2}{3})^2 = \frac{40}{243}$,$P(X = 1) = C_{5}^{1}×(\frac{1}{3})^1×(\frac{2}{3})^4 = \frac{80}{243}$,$P(X = 3) = C_{5}^{2}×(\frac{1}{3})^2×(\frac{2}{3})^3 = \frac{80}{243}$,$P(X = 5) = C_{5}^{0}×(\frac{1}{3})^0×(\frac{2}{3})^5 = \frac{32}{243}$. 所以随机变量$X$的分布列为

所以随机变量$X$的数学期望为$E(X) = (-5)×\frac{1}{243} +$
$(-3)×\frac{10}{243} + (-1)×\frac{40}{243} + 1×\frac{80}{243} + 3×\frac{80}{243} + 5×\frac{32}{243} = \frac{5}{3}$.
5. 解:
(1) 当$n = 4$时,质点所能到达的数$X$必满足$\vert X\vert\leq4$且$X$为偶数.若$X = - 2$,则表示该质点向右移动$1$次,向左移动$3$次.所以$P(X = - 2) = C_{4}^{3}×(\frac{1}{3})^3×\frac{2}{3} = \frac{8}{81}$.所以$P(X > 0) = P(X = 2) + P(X = 4) = C_{4}^{1}×\frac{1}{3}×(\frac{2}{3})^3 + C_{4}^{0}×(\frac{2}{3})^4 = \frac{32}{81} + \frac{16}{81} = \frac{16}{27}$.
(2) 当$n = 5$时,质点所能到达的数$X$必满足$\vert X\vert\leq5$且$X$为奇数,所以随机变量$X$的所有可能取值为$- 5$,$- 3$,$- 1$,$1$,$3$,$5$.所以$P(X = - 5) = C_{5}^{5}×(\frac{1}{3})^5 = \frac{1}{243}$,$P(X = - 3) = C_{5}^{4}×(\frac{1}{3})^4×\frac{2}{3} = \frac{10}{243}$,$P(X = - 1) = C_{5}^{3}×(\frac{1}{3})^3×(\frac{2}{3})^2 = \frac{40}{243}$,$P(X = 1) = C_{5}^{1}×(\frac{1}{3})^1×(\frac{2}{3})^4 = \frac{80}{243}$,$P(X = 3) = C_{5}^{2}×(\frac{1}{3})^2×(\frac{2}{3})^3 = \frac{80}{243}$,$P(X = 5) = C_{5}^{0}×(\frac{1}{3})^0×(\frac{2}{3})^5 = \frac{32}{243}$. 所以随机变量$X$的分布列为

所以随机变量$X$的数学期望为$E(X) = (-5)×\frac{1}{243} +$
$(-3)×\frac{10}{243} + (-1)×\frac{40}{243} + 1×\frac{80}{243} + 3×\frac{80}{243} + 5×\frac{32}{243} = \frac{5}{3}$.
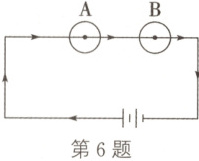
6. (多选题)如图,某电子实验猫线路图上有A,B
两个红绿指示灯,当遇到红灯时,实验猫停止
前行,恢复绿灯后,继续
前行,A,B两个指示灯工作相互独立,且出
现红灯的概率分别为$\frac{1}{3},p(0<p<1)$.同学
甲将从第一次试验到第五次试验中,实验猫
在A处遇到红灯的次数记为$X$,同一次试验
中在A,B两处遇到红灯的次数之和记为$Y$,
则下列结论正确的是
(
A.$P(X=3)=\frac{80}{243}$
B.一次试验中,A,B两处至少遇到一次红灯
的概率为$\frac{1}{3}+\frac{2}{3}p$
C.$D(X)=\frac{8}{9}$
D.当$p=\frac{2}{5}$时,$E(Y)=\frac{11}{15}$
两个红绿指示灯,当遇到红灯时,实验猫停止
前行,恢复绿灯后,继续
前行,A,B两个指示灯工作相互独立,且出
现红灯的概率分别为$\frac{1}{3},p(0<p<1)$.同学
甲将从第一次试验到第五次试验中,实验猫
在A处遇到红灯的次数记为$X$,同一次试验
中在A,B两处遇到红灯的次数之和记为$Y$,
则下列结论正确的是
(
BD
)
A.$P(X=3)=\frac{80}{243}$
B.一次试验中,A,B两处至少遇到一次红灯
的概率为$\frac{1}{3}+\frac{2}{3}p$
C.$D(X)=\frac{8}{9}$
D.当$p=\frac{2}{5}$时,$E(Y)=\frac{11}{15}$
答案:
6.BD
查看更多完整答案,请扫码查看


