2025年通成学典课时作业本高中数学选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通成学典课时作业本高中数学选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 对某地区过去 20 年的年降水量(单位:毫米)
进行统计,得到以下数据:887,939,643,996,
715,838,1 082,923,901,1 182,1 035,863,
772,943,1 035,1 022,855,1 118,768,809.将
年降水量处于 800 毫米以下、800~1 000 毫
米、1 000 毫米以上分别指定为年降水量偏
少、适中、偏多三个等级.
(1)用年降水量处于各等级的频率估计概
率,分别计算该地区年降水量偏少、适中、偏
多的概率.
(2)根据经验,种植甲、乙、丙三种农作物在
年降水量偏少、适中、偏多的情况下可产出的
年利润(单位:千元/公顷)如下表:

你认为这三种作物中,哪一种最适合在该地
区推广种植?请说明理由.
进行统计,得到以下数据:887,939,643,996,
715,838,1 082,923,901,1 182,1 035,863,
772,943,1 035,1 022,855,1 118,768,809.将
年降水量处于 800 毫米以下、800~1 000 毫
米、1 000 毫米以上分别指定为年降水量偏
少、适中、偏多三个等级.
(1)用年降水量处于各等级的频率估计概
率,分别计算该地区年降水量偏少、适中、偏
多的概率.
(2)根据经验,种植甲、乙、丙三种农作物在
年降水量偏少、适中、偏多的情况下可产出的
年利润(单位:千元/公顷)如下表:

你认为这三种作物中,哪一种最适合在该地
区推广种植?请说明理由.
答案:
1. 解:
(1) 将过去20年的年降水量按照降水量等级分类,年降水量偏少的有4年,概率可估计为$\frac{4}{20}=0.2;$年降水量适中的有10年,概率可估计为$\frac{10}{20}=0.5;$年降水量偏多的有6年,概率可估计为$\frac{6}{20}=0.3.$所以该地区年降水量偏少、适中、偏多的概率分别为0.2,0.5,0.3.
(2) 作物丙最适合在该地区推广种植.理由:设种植农作物甲、乙、丙一年后每公顷获得的利润分别是随机变量X,Y,Z(单位:千元),则X的分布列为

E(X)=8×0.5+12×0.5=10.Y的分布列为
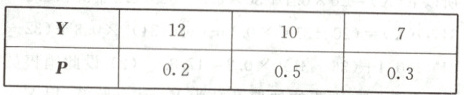
E(Y)=12×0.2+10×0.5+7×0.3=9.5.Z的分布列为

E(Z)=7×0.2+10×0.5+12×0.3=10.所以E(Y)<E(X)=E(Z),即种植作物甲、丙产出的年利润的期望值比作物乙更高.故不考虑推广作物乙.又D(X)=0.5×(8-10)^2+0.5×(12-10)^2=4,D(Z)=0.2×(7-10)^2+0.5×(10-10)^2+0.3×(12-10)^2=3,D(X)>D(Z),所以种植作物丙产出的年利润的稳定性更好.故作物丙最适合在该地区推广种植.
1. 解:
(1) 将过去20年的年降水量按照降水量等级分类,年降水量偏少的有4年,概率可估计为$\frac{4}{20}=0.2;$年降水量适中的有10年,概率可估计为$\frac{10}{20}=0.5;$年降水量偏多的有6年,概率可估计为$\frac{6}{20}=0.3.$所以该地区年降水量偏少、适中、偏多的概率分别为0.2,0.5,0.3.
(2) 作物丙最适合在该地区推广种植.理由:设种植农作物甲、乙、丙一年后每公顷获得的利润分别是随机变量X,Y,Z(单位:千元),则X的分布列为

E(X)=8×0.5+12×0.5=10.Y的分布列为

E(Y)=12×0.2+10×0.5+7×0.3=9.5.Z的分布列为

E(Z)=7×0.2+10×0.5+12×0.3=10.所以E(Y)<E(X)=E(Z),即种植作物甲、丙产出的年利润的期望值比作物乙更高.故不考虑推广作物乙.又D(X)=0.5×(8-10)^2+0.5×(12-10)^2=4,D(Z)=0.2×(7-10)^2+0.5×(10-10)^2+0.3×(12-10)^2=3,D(X)>D(Z),所以种植作物丙产出的年利润的稳定性更好.故作物丙最适合在该地区推广种植.
2. 某经营礼品花卉的店主记录了去年当中 100 天
的 A,B 两种花卉每枝的收益情况,如下表:
A 种花卉:
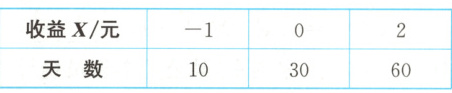
B 种花卉:

(1)如果店主向你咨询,明年只经营一种花
卉,你会给出怎样的建议呢?
(2)在实际中可以选择适当的比例经营这两
种花卉,假设两种花卉的进货价都是每枝
1 元,店主计划投入 10 000 元,请你给出一个
经营方案,并说明理由.
的 A,B 两种花卉每枝的收益情况,如下表:
A 种花卉:

B 种花卉:

(1)如果店主向你咨询,明年只经营一种花
卉,你会给出怎样的建议呢?
(2)在实际中可以选择适当的比例经营这两
种花卉,假设两种花卉的进货价都是每枝
1 元,店主计划投入 10 000 元,请你给出一个
经营方案,并说明理由.
答案:
2. 解:
(1) A种花卉的收益X可能的取值有-1,0,2,则$P(X=-1)=\frac{10}{100}=0.1,P(X=0)=\frac{30}{100}=0.3,P(X=2)=\frac{60}{100}=0.6,$所以$E(X)=-1×0.1+0×0.3+2×0.6=1.1,D(X)=0.1×(-1-1.1)^2+0.3×(0-1.1)^2+0.6×(2-1.1)^2=1.29.B$种花卉的收益Y可能的取值有0,1,2,则$P(Y=0)=\frac{30}{100}=0.3,P(Y=1)=\frac{30}{100}=0.3,P(Y=2)=\frac{40}{100}=0.4,$所以$E(Y)=0×0.3+1×0.3+2×0.4=1.1,D(Y)=0.3×(0-1.1)^2+0.3×(1-1.1)^2+0.4×(2-1.1)^2=0.69.$因为E(X)=E(Y),D(X)>D(Y),所以B种花卉的收益较为稳定.故建议选择经营B种花卉.
(2) 经营方案:投入3485元经营A种花卉,投入6515元经营B种花卉.理由:设投入a元经营A种花卉,则投入(10000-a)元经营B种花卉.E(aX)+E[(10000-a)Y]=aE(X)+(10000-a)E(Y)=11000,$D(aX)+D[(10000-a)Y]=a^2D(X)+(10000-a)^2·D(Y)=1.29a^2+0.69(10000-a)^2=1.98a^2-13800a+0.69×10^8,$易知当$a=\frac{-(-13800)}{2×1.98}≈3485$时,经营两种花卉的收益的方差最小,收益最稳定.10000-3485=6515(元),所以投入3485元经营A种花卉,投入6515元经营B种花卉.
(1) A种花卉的收益X可能的取值有-1,0,2,则$P(X=-1)=\frac{10}{100}=0.1,P(X=0)=\frac{30}{100}=0.3,P(X=2)=\frac{60}{100}=0.6,$所以$E(X)=-1×0.1+0×0.3+2×0.6=1.1,D(X)=0.1×(-1-1.1)^2+0.3×(0-1.1)^2+0.6×(2-1.1)^2=1.29.B$种花卉的收益Y可能的取值有0,1,2,则$P(Y=0)=\frac{30}{100}=0.3,P(Y=1)=\frac{30}{100}=0.3,P(Y=2)=\frac{40}{100}=0.4,$所以$E(Y)=0×0.3+1×0.3+2×0.4=1.1,D(Y)=0.3×(0-1.1)^2+0.3×(1-1.1)^2+0.4×(2-1.1)^2=0.69.$因为E(X)=E(Y),D(X)>D(Y),所以B种花卉的收益较为稳定.故建议选择经营B种花卉.
(2) 经营方案:投入3485元经营A种花卉,投入6515元经营B种花卉.理由:设投入a元经营A种花卉,则投入(10000-a)元经营B种花卉.E(aX)+E[(10000-a)Y]=aE(X)+(10000-a)E(Y)=11000,$D(aX)+D[(10000-a)Y]=a^2D(X)+(10000-a)^2·D(Y)=1.29a^2+0.69(10000-a)^2=1.98a^2-13800a+0.69×10^8,$易知当$a=\frac{-(-13800)}{2×1.98}≈3485$时,经营两种花卉的收益的方差最小,收益最稳定.10000-3485=6515(元),所以投入3485元经营A种花卉,投入6515元经营B种花卉.
查看更多完整答案,请扫码查看


