2025年通成学典课时作业本高中数学选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通成学典课时作业本高中数学选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 若随机变量 $X$ 的分布列为

则 $D(X)$ 等于 (
A.$0.5$
B.$0.42$
C.$0.24$
D.$0.16$

则 $D(X)$ 等于 (
C
)A.$0.5$
B.$0.42$
C.$0.24$
D.$0.16$
答案:
1. C
2. (2024·郑州期末) 已知随机变量 $X$ 满足 $D(2 - 2X) = 4$,则下列结论正
A.$D(X) = - 1$
B.$D(X) = 1$
C.$D(X) = 4$
D.$D(X) = 2$
确
的是 (B
)A.$D(X) = - 1$
B.$D(X) = 1$
C.$D(X) = 4$
D.$D(X) = 2$
答案:
2. B
3. (多选题)(2025·温州期中) 离散型随机变量 $X$ 的分布列为

若离散型随机变量 $Y$ 满足 $Y = 2X + 1$,则下列说法正确的是 (
A.$m = 0.1$
B.$P(|X - 2| = 1) = 0.6$
C.$E(X) = 2,D(X) = 1.8$
D.$E(Y) = 5,D(Y) = 8.2$

若离散型随机变量 $Y$ 满足 $Y = 2X + 1$,则下列说法正确的是 (
ABC
)A.$m = 0.1$
B.$P(|X - 2| = 1) = 0.6$
C.$E(X) = 2,D(X) = 1.8$
D.$E(Y) = 5,D(Y) = 8.2$
答案:
3. ABC
4. (2025·广西期中) 若 $D(X) = 9$,则 $\sigma(X) =$
3
,$D(3X - 2) =$ 81
.
答案:
4. 3 81
5. 甲、乙两人进行定点投篮游戏,投篮者若投中,则继续投篮,否则由对方投篮,第一次由甲投篮. 已知每次投篮甲、乙两人投中的概率分别为 $\frac{1}{3},\frac{3}{4}$.
(1) 求第三次由乙投篮的概率;
(2) 在前 $3$ 次投篮中,乙投篮的次数为 $\xi$,求 $\xi$ 的分布列;
(3) 求 (2) 中 $\xi$ 的数学期望及标准差.
(1) 求第三次由乙投篮的概率;
(2) 在前 $3$ 次投篮中,乙投篮的次数为 $\xi$,求 $\xi$ 的分布列;
(3) 求 (2) 中 $\xi$ 的数学期望及标准差.
答案:
5. 解:
(1) 因为第三次由乙投篮包括第一次甲投中、第二次甲未投中和第一次甲未投中、第二次乙投中,所以第三次由乙投篮的概率为$\frac{1}{3} × \frac{2}{3} + \frac{2}{3} × \frac{3}{4} = \frac{13}{18} (2) $由题意可知,$\xi $的所有可能取值为 0,1,2,则$ P(\xi = 0) = \frac{1}{3} ×$
$\frac{1}{3} = \frac{1}{9},$$P(\xi = 1) = \frac{1}{3} × \frac{2}{3} + \frac{2}{3} × \frac{1}{4} = \frac{7}{18},$$P(\xi = 2) =$
$\frac{2}{3} × \frac{3}{4} = \frac{1}{2} $所以$ \xi $的分布列为
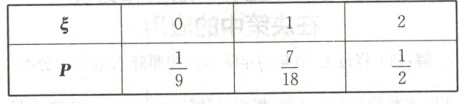
(3) 由
(2)知,$E(\xi) = 0 × \frac{1}{9} + 1 × \frac{7}{18} + 2 × \frac{1}{2} = \frac{25}{18},$所以
$D(\xi) = (0 - \frac{25}{18})^2 × \frac{1}{9} + (1 - \frac{25}{18})^2 × \frac{7}{18} + (2 - \frac{25}{18})^2 ×$
$\frac{1}{2} = \frac{149}{324} $所以$ \sqrt{D(\xi)} = \frac{\sqrt{149}}{18}$
5. 解:
(1) 因为第三次由乙投篮包括第一次甲投中、第二次甲未投中和第一次甲未投中、第二次乙投中,所以第三次由乙投篮的概率为$\frac{1}{3} × \frac{2}{3} + \frac{2}{3} × \frac{3}{4} = \frac{13}{18} (2) $由题意可知,$\xi $的所有可能取值为 0,1,2,则$ P(\xi = 0) = \frac{1}{3} ×$
$\frac{1}{3} = \frac{1}{9},$$P(\xi = 1) = \frac{1}{3} × \frac{2}{3} + \frac{2}{3} × \frac{1}{4} = \frac{7}{18},$$P(\xi = 2) =$
$\frac{2}{3} × \frac{3}{4} = \frac{1}{2} $所以$ \xi $的分布列为

(3) 由
(2)知,$E(\xi) = 0 × \frac{1}{9} + 1 × \frac{7}{18} + 2 × \frac{1}{2} = \frac{25}{18},$所以
$D(\xi) = (0 - \frac{25}{18})^2 × \frac{1}{9} + (1 - \frac{25}{18})^2 × \frac{7}{18} + (2 - \frac{25}{18})^2 ×$
$\frac{1}{2} = \frac{149}{324} $所以$ \sqrt{D(\xi)} = \frac{\sqrt{149}}{18}$
6. 已知随机变量 $\xi$ 的分布列为
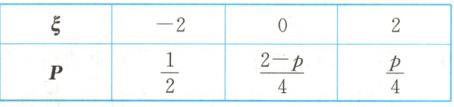
随机变量 $\eta$ 的分布列为
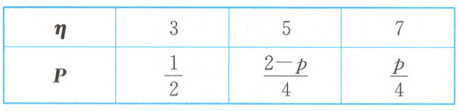
则下列结论正确的是 (
A.$E(\xi) = E(\eta)$
B.当 $p$ 增大时, $E(\xi)$ 递减
C.$D(\xi) > D(\eta)$
D.当 $p$ 增大时, $D(\eta)$ 递增

随机变量 $\eta$ 的分布列为

则下列结论正确的是 (
D
)A.$E(\xi) = E(\eta)$
B.当 $p$ 增大时, $E(\xi)$ 递减
C.$D(\xi) > D(\eta)$
D.当 $p$ 增大时, $D(\eta)$ 递增
答案:
6. D
7. (2025·连云港期中) 已知随机变量 $X$ 满足:$P(X = x_i) = \frac{1}{n}(i = 1,2,·s,n)$,当 $i \leq n - 1$ 时,$x_i < x_{i + 1}$,随机变量 $Y$ 的取值为 $y_1 = \frac{x_1 + x_2}{2},y_2 = \frac{x_2 + x_3}{2},·s,y_{n - 1} = \frac{x_{n - 1} + x_n}{2},y_n = \frac{x_n + x_1}{2}$,且 $P(Y = y_i) = \frac{1}{n}(i = 1,2,·s,n)$,则下列结论正确的是 (
A.$E(X) < E(Y)$
B.$E(X) > E(Y)$
C.$D(X) < D(Y)$
D.$D(X) > D(Y)$
D
)A.$E(X) < E(Y)$
B.$E(X) > E(Y)$
C.$D(X) < D(Y)$
D.$D(X) > D(Y)$
答案:
7. D
8. (多选题)(2025·惠州阶段练习) 将 $x,x,y,y,z,z$ 填入 $2$ 行 $3$ 列的表格中,每格填一个字母. 若随机变量 $X$ 表示列字母相同的数量,则下列说法正确的是 (
A.$X$ 的所有可能取值有 $0,1,3$
B.$P(X = 0) = \frac{8}{15}$
C.$E(X) = \frac{3}{5}$
D.$D(X) = \frac{12}{25}$
ABC
)A.$X$ 的所有可能取值有 $0,1,3$
B.$P(X = 0) = \frac{8}{15}$
C.$E(X) = \frac{3}{5}$
D.$D(X) = \frac{12}{25}$
答案:
8. ABC
查看更多完整答案,请扫码查看


