《2025年通成学典课时作业本高中数学选择性必修第三册人教版》

9. 已知$P(A) = 0.6$，$P(B|A) = 0.3$，$P(B|\overline{A}) = 0.2$，则$P(B) =$ 0.26.

答案： 9. 0.26

10. 清明节前夕，某校团委决定举办“缅怀革命先烈，致敬时代英雄”主题演讲比赛，经过初赛，共 7 人进入决赛，其中高一年级 2 人，高二年级 3 人，高三年级 2 人，现采取抽签方式决定演讲顺序，设事件 A 为“高二年级 3 人相邻”，事件 A 的排法有 720 种; 在事件 A“高二年级 3 人相邻”发生的前提下，事件 B“高一年级 2 人不相邻”发生的概率为 $\frac{3}{5}$.

答案： $10. 720 \frac{3}{5}$

11.(2025·沧州阶段练习)某学校门口设置了限时停车场，制定收费标准如下：停车时间不超过 15 分钟免费，超过 15 分钟但不超过 30 分钟收费 5 元，超过 30 分钟但不超过 45 分钟收费 15 元，超过 45 分钟但不超过 60 分钟收费 30 元，超过 60 分钟必须离开停车场. 甲、乙两位家长相互独立地来该停车场停车，且甲、乙的停车时间的概率如下表：

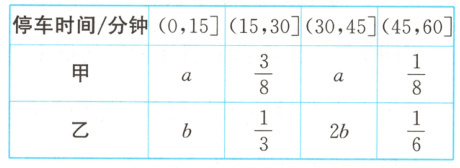
(1) 求甲所付停车费用小于乙所付停车费用的概率.
(2) 设甲所付停车费用为 X 元，乙所付停车费用为 Y 元. 在$X + Y = 30$的条件下，求$X = Y$的概率.

答案： 11. 解：（1）由题意，可得$a+a=\frac{1}{2}，$$b+2b=\frac{1}{2}，$所以$a=\frac{1}{4}，$$b=\frac{1}{6}。$甲所付停车费用小于乙所付停车费用有下列情况：甲(0,15]，乙(15,30]或(30,45]或(45,60]，概率为$\frac{1}{4}×(\frac{1}{3}+\frac{1}{3}+\frac{1}{6})=\frac{5}{24}；$甲(15,30]，乙(30,45]或(45,60]，概率为$\frac{3}{8}×(\frac{1}{3}+\frac{1}{6})=\frac{3}{16}；$甲(30,45]，乙(45,60]，概率为$\frac{1}{4}×\frac{1}{6}=\frac{1}{24}。$所以甲所付停车费用小于乙所付停车费用的概率为$\frac{5}{24}+\frac{3}{16}+\frac{1}{24}=\frac{7}{16}。$（2）X+Y=30有下列情况：甲(0,15]，乙(45,60]，概率为$\frac{1}{4}×\frac{1}{6}=\frac{1}{24}；$甲(30,45]，乙(30,45]，概率为$\frac{1}{4}×\frac{1}{3}=\frac{1}{12}；$甲(45,60]，乙(0,15]，概率为$\frac{1}{8}×\frac{1}{6}=\frac{1}{48}。$所以$P(X+Y=30)=\frac{1}{24}+\frac{1}{12}+\frac{1}{48}=\frac{7}{48}。$又因为P(X+Y=30且$X=Y)=\frac{1}{4}×\frac{1}{3}-\frac{1}{12}，$所以P(X=Y|$X+Y=30)=\frac{\frac{1}{12}}{\frac{7}{48}}=\frac{4}{7}。$

12. 核心素养 逻辑推理 (2024·吉林期末)甲、乙两名同学进行轮流投篮比赛，为了增加趣味性，设计了如下方案：若投中，自己得 1 分，对方得 0 分; 若投不中，自己得 0 分，对方得 1 分. 已知甲投篮投中的概率为$\frac {2}{3}$，乙投篮投中的概率为$\frac {1}{2}$. 由甲先投篮，无论谁投篮，每投一次为一轮比赛，规定当一人比另一人多 2 分或进行完 5 轮投篮后，活动结束，得分多的一人获胜，且两人投篮投中与否相互独立.
(1) 在结束时甲获胜的条件下，求甲比乙多 2 分的概率.
(2) 已知在改变比赛规则的条件下，乙获胜的概率大于在原规则的条件下乙获胜的概率. 设事件 R = “改变比赛规则”，事件 S = “乙获胜”. 若$0 ＜ P(S) ＜ 1$，求证：$P(R|\overline{S}) ＞ P(R|\overline{S})$.

答案： 12. 解：（1）记“甲投篮投中”为事件A，“乙投篮投中”为事件B，“结束时甲获胜”为事件M.事件M发生有下列情况：2轮结束或4轮结束或5轮结束，即甲与乙的比分为2:0或3:1或3:2结束比赛.若甲与乙的比分为2:0，则$P_1=P(AB)=\frac{2}{3}×\frac{1}{2}×\frac{1}{3}=\frac{1}{3}；$若甲与乙的比分为3:1，则 $ P_{2}=P(ABAB + \overline{A}B\overline{A}B)=\frac{2}{3}×\frac{1}{2}×\frac{2}{3}×\frac{1}{2}+\frac{1}{3}×\frac{1}{2}×\frac{2}{3}×\frac{1}{2}=\frac{1}{6} $；若甲与乙的比分为 $ 3:2 $，则 $ P_{3}=P(ABABA+\overline{A}BABA+AB\overline{A}BA+\overline{A}B\overline{A}BA)=(\frac{2}{3})^{3}×(\frac{1}{2})^{2}+(\frac{2}{3})^{2}×\frac{1}{3}×(\frac{1}{2})^{2}×2+(\frac{1}{3})^{2}×(\frac{1}{2})^{2}×\frac{2}{3}=\frac{1}{6} $。所以 $ P(M)=P_{1}+P_{2}+P_{3}=\frac{2}{3} $。设“结束时甲比乙多 $ 2 $ 分”为事件 $ N $，则 $ P(MN)=P_{1}+P_{2}=\frac{1}{2} $，所以 $ P(N|M)=\frac{P(MN)}{P(M)}=\frac{3}{4} $，即在结束时甲获胜的条件下，甲比乙多 $ 2 $ 分的概率为 $ \frac{3}{4} $。
（2）证明：因为在改变比赛规则的条件下，乙获胜的概率大于在原规则的条件下乙获胜的概率，所以 $ P(S|R)＞P(S|\overline{R}) $，即 $ \frac{P(RS)}{P(R)}＞\frac{P(\overline{R}S)}{P(\overline{R})} $。因为 $ P(R)＞0,P(\overline{R})＞0 $，所以 $ P(RS)P(\overline{R})＞P(\overline{R}S)P(R) $。因为 $ P(\overline{R})=1 - P(R),P(\overline{R}S)=P(S)-P(RS) $，所以 $ P(RS)[1 - P(R)]＞[P(S)-P(RS)]P(R) $。所以 $ P(RS)＞P(R)P(S) $。所以 $ P(RS)-P(RS)P(S)＞P(R)P(S)-P(RS)P(S) $，即 $ P(RS)[1 - P(S)]＞P(S)[P(R)-P(RS)] $。又因为 $ 1 - P(S)=P(\overline{S}) $，$ P(R)-P(RS)=P(R\overline{S}) $，所以 $ P(RS)P(\overline{S})＞P(S)P(R\overline{S}) $。因为 $ 0＜P(S)＜1 $，则 $ 0＜P(\overline{S})＜1 $，所以 $ \frac{P(RS)}{P(S)}＞\frac{P(R\overline{S})}{P(\overline{S})} $，即 $ P(R|S)＞P(R|\overline{S}) $。