2025年通成学典课时作业本高中数学选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通成学典课时作业本高中数学选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
9. (2025·新课标Ⅰ卷)一个不透明的箱子里有$5$个相同的球,分别以$1\sim5$标号,若每次取一个球,有放回地取三次,记至少取出一次的球的个数为$X$,则$E(X) =$
$\frac{61}{25}$
.
答案:
9.$\frac{61}{25}$
10. (2024·南宁阶段练习)某APP举行推广活动,新用户注册前$7$天内,每天登录可获得$1$元红包,前$7$天连续登录的新用户,还可进入抽奖活动页面领取红包,每位用户随机点击$4$个红包中的$1$个领取(领取前不知道红包金额),领取后看一分钟广告,可再次从剩余$3$个红包中领取$1$个,这$4$个红包的金额分别为$a$元、$a$元、$2a$元、$3a$元($a > 0$).
(1) 若前$7$天连续登录且抽奖活动页面看一分钟广告的新用户获得的所有红包金额之和$X$(单位:元)的期望为$70$,求$a$的值.
(2) 该APP推广活动进行一个月后,对新用户登录方案进行了调整:新用户注册前$7$天内,连续登录第$i$天,当天可获得$i$元红包,中间中断再登录重新计算连续天数.若某新注册用户前$4$天已经连续登录该APP,后$3$天每天登录的概率均为$\frac{1}{2}$,求该用户前$7$天内通过登录获得的红包金额之和$Y$(单位:元)的分布列.
(1) 若前$7$天连续登录且抽奖活动页面看一分钟广告的新用户获得的所有红包金额之和$X$(单位:元)的期望为$70$,求$a$的值.
(2) 该APP推广活动进行一个月后,对新用户登录方案进行了调整:新用户注册前$7$天内,连续登录第$i$天,当天可获得$i$元红包,中间中断再登录重新计算连续天数.若某新注册用户前$4$天已经连续登录该APP,后$3$天每天登录的概率均为$\frac{1}{2}$,求该用户前$7$天内通过登录获得的红包金额之和$Y$(单位:元)的分布列.
答案:
10. 解:
(1)由题意,得$X$的可能取值为$2a+7,3a+7,4a+7,5a+7$,所以$P(X=2a+7)=\frac{1}{C_4^2}=\frac{1}{6}$,$P(X=3a+7)=\frac{2}{C_4^2}=\frac{1}{3}$,$P(X=4a+7)=\frac{2}{C_4^2}=\frac{1}{3}$,$P(X=5a+7)=\frac{1}{C_4^2}=\frac{1}{6}$,所以$E(X)=(2a+7)×\frac{1}{6}+(3a+7)×\frac{1}{3}+(4a+7)×\frac{1}{3}+(5a+7)×\frac{1}{6}=70$,解得$a=18$.
(2)易知该用户前4天获得的红包金额之和为$1+2+3+4=10$(元).由题意,得$Y$的可能取值为$10,11,13,15,16,21,28$,则$P(Y=10)=(1-\frac{1}{2})^3=\frac{1}{8}$,$P(Y=11)=(1-\frac{1}{2})×\frac{1}{2}×(1-\frac{1}{2})+(1-\frac{1}{2})×(1-\frac{1}{2})×\frac{1}{2}=\frac{1}{4}$,$P(Y=13)=(1-\frac{1}{2})×\frac{1}{2}×\frac{1}{2}=\frac{1}{8}$,$P(Y=15)=\frac{1}{2}×(1-\frac{1}{2})×(1-\frac{1}{2})=\frac{1}{8}$,$P(Y=16)=\frac{1}{2}×(1-\frac{1}{2})×(1-\frac{1}{2})=\frac{1}{8}$,$P(Y=21)=\frac{1}{2}×\frac{1}{2}×(1-\frac{1}{2})=\frac{1}{8}$,$P(Y=28)=\frac{1}{2}×\frac{1}{2}×\frac{1}{2}=\frac{1}{8}$,所以$Y$的分布列为
$\begin{matrix}Y&10&11&13&15&16&21&28\\P&\frac{1}{8}&\frac{1}{4}&\frac{1}{8}&\frac{1}{8}&\frac{1}{8}&\frac{1}{8}&\frac{1}{8}\end{matrix}$
(1)由题意,得$X$的可能取值为$2a+7,3a+7,4a+7,5a+7$,所以$P(X=2a+7)=\frac{1}{C_4^2}=\frac{1}{6}$,$P(X=3a+7)=\frac{2}{C_4^2}=\frac{1}{3}$,$P(X=4a+7)=\frac{2}{C_4^2}=\frac{1}{3}$,$P(X=5a+7)=\frac{1}{C_4^2}=\frac{1}{6}$,所以$E(X)=(2a+7)×\frac{1}{6}+(3a+7)×\frac{1}{3}+(4a+7)×\frac{1}{3}+(5a+7)×\frac{1}{6}=70$,解得$a=18$.
(2)易知该用户前4天获得的红包金额之和为$1+2+3+4=10$(元).由题意,得$Y$的可能取值为$10,11,13,15,16,21,28$,则$P(Y=10)=(1-\frac{1}{2})^3=\frac{1}{8}$,$P(Y=11)=(1-\frac{1}{2})×\frac{1}{2}×(1-\frac{1}{2})+(1-\frac{1}{2})×(1-\frac{1}{2})×\frac{1}{2}=\frac{1}{4}$,$P(Y=13)=(1-\frac{1}{2})×\frac{1}{2}×\frac{1}{2}=\frac{1}{8}$,$P(Y=15)=\frac{1}{2}×(1-\frac{1}{2})×(1-\frac{1}{2})=\frac{1}{8}$,$P(Y=16)=\frac{1}{2}×(1-\frac{1}{2})×(1-\frac{1}{2})=\frac{1}{8}$,$P(Y=21)=\frac{1}{2}×\frac{1}{2}×(1-\frac{1}{2})=\frac{1}{8}$,$P(Y=28)=\frac{1}{2}×\frac{1}{2}×\frac{1}{2}=\frac{1}{8}$,所以$Y$的分布列为
$\begin{matrix}Y&10&11&13&15&16&21&28\\P&\frac{1}{8}&\frac{1}{4}&\frac{1}{8}&\frac{1}{8}&\frac{1}{8}&\frac{1}{8}&\frac{1}{8}\end{matrix}$
11. 甲、乙两人做游戏,每次游戏只需用一只手参与,记甲的左、右手分别为$s_1,s_2$,乙的左、右手分别为$t_1,t_2$,每次游戏甲、乙两人的得分之和均为$0$,记甲用$s_1$的概率为$x$($0\leqslant x\leqslant1$),乙用$t_1$的概率为$y$($0\leqslant y\leqslant1$),每次游戏甲的得分如下表:

(1) 分别求每次游戏甲得分的期望与乙得分的期望;
(2) 当$x = \frac{1}{2},y = \frac{1}{3}$时,设每次游戏甲、乙两人选择用哪只手参与相互独立,求经过两次游戏后,乙的总得分为正数的概率;
(3) 假设$x,y$的值可以自由调整,其中$x$不取$\frac{1}{4}$,求证:不论$y$取何值,甲总能通过调整$x$的值,使得每次游戏甲得分的期望不小于$\frac{1}{2}$.

(1) 分别求每次游戏甲得分的期望与乙得分的期望;
(2) 当$x = \frac{1}{2},y = \frac{1}{3}$时,设每次游戏甲、乙两人选择用哪只手参与相互独立,求经过两次游戏后,乙的总得分为正数的概率;
(3) 假设$x,y$的值可以自由调整,其中$x$不取$\frac{1}{4}$,求证:不论$y$取何值,甲总能通过调整$x$的值,使得每次游戏甲得分的期望不小于$\frac{1}{2}$.
答案:
11.解:
(1)设每次游戏甲的得分为$X$,乙的得分为$Y.X$的分布列为

所以$E(X)=5xy - 7x(1 - y)-(1 - x)y+3(1 - x)(1 - y)=16xy - 10x - 4y+3$,则$E(Y)=-E(X)=-16xy + 10x + 4y - 3$.
(2)当$x=\frac{1}{2},y=\frac{1}{3}$时,$Y$的分布列为
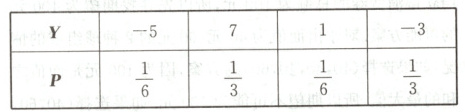
当乙第一次得7分时,第二次不管得几分,乙的总得分均为正数;当乙第一次得$-5$分或$-3$分时,第二次只能得7分;当乙第一次得1分时,第二次只能得1分或7分.故经过两次游戏后,乙的总得分为正数的概率为$\frac{1}{3}+(\frac{1}{6}+\frac{1}{3})×\frac{1}{3}+\frac{1}{6}×(\frac{1}{6}+\frac{1}{3})=\frac{7}{12}$.
(3)证明:记$E(X)=f(x,y)=(16y - 10)x - 4y+3(0\leq x\leq1且x\neq\frac{1}{4})$.当$y=\frac{5}{8}$时,$E(X)=-4×\frac{5}{8}+3=\frac{1}{2}$;当$y\in[0,\frac{5}{8})$时,$16y - 10<0$,$f(x)$单调递减,则甲可取$x = 0$,使得$E(X)=f(0)=-4y+3>\frac{1}{2}$;当$y\in(\frac{5}{8},1]$时,$16y - 10>0$,$f(x)$单调递增,则甲可取$x = 1$,使得$E(X)=f(1)=12y - 7>\frac{1}{2}$.综上所述,不论$y$取何值,甲总能通过调整$x$的值,使得每次游戏甲得分的期望不小于$\frac{1}{2}$.
11.解:
(1)设每次游戏甲的得分为$X$,乙的得分为$Y.X$的分布列为

所以$E(X)=5xy - 7x(1 - y)-(1 - x)y+3(1 - x)(1 - y)=16xy - 10x - 4y+3$,则$E(Y)=-E(X)=-16xy + 10x + 4y - 3$.
(2)当$x=\frac{1}{2},y=\frac{1}{3}$时,$Y$的分布列为

当乙第一次得7分时,第二次不管得几分,乙的总得分均为正数;当乙第一次得$-5$分或$-3$分时,第二次只能得7分;当乙第一次得1分时,第二次只能得1分或7分.故经过两次游戏后,乙的总得分为正数的概率为$\frac{1}{3}+(\frac{1}{6}+\frac{1}{3})×\frac{1}{3}+\frac{1}{6}×(\frac{1}{6}+\frac{1}{3})=\frac{7}{12}$.
(3)证明:记$E(X)=f(x,y)=(16y - 10)x - 4y+3(0\leq x\leq1且x\neq\frac{1}{4})$.当$y=\frac{5}{8}$时,$E(X)=-4×\frac{5}{8}+3=\frac{1}{2}$;当$y\in[0,\frac{5}{8})$时,$16y - 10<0$,$f(x)$单调递减,则甲可取$x = 0$,使得$E(X)=f(0)=-4y+3>\frac{1}{2}$;当$y\in(\frac{5}{8},1]$时,$16y - 10>0$,$f(x)$单调递增,则甲可取$x = 1$,使得$E(X)=f(1)=12y - 7>\frac{1}{2}$.综上所述,不论$y$取何值,甲总能通过调整$x$的值,使得每次游戏甲得分的期望不小于$\frac{1}{2}$.
查看更多完整答案,请扫码查看


