2025年通成学典课时作业本高中数学选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通成学典课时作业本高中数学选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. (2025·山东期中)已知随机变量$X$服从两点分布,且$P(X = 0) = 0.4$.设$Y = 3X - 2$,则$P(Y = 1)$等于 (
A.0.2
B.0.3
C.0.4
D.0.6
D
)A.0.2
B.0.3
C.0.4
D.0.6
答案:
8.D
9. (多选题)已知随机变量$\xi$的分布列为
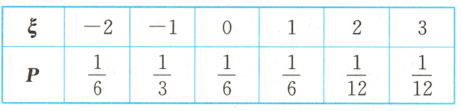
若$P(\xi^2 < x) = \frac{2}{3}$,则实数$x$的值可能是
(
A.1
B.2
C.3
D.4

若$P(\xi^2 < x) = \frac{2}{3}$,则实数$x$的值可能是
(
BCD
)A.1
B.2
C.3
D.4
答案:
9.BCD
10. (2025·宁波期中)已知某兴趣小组内学舞蹈且不学声乐的有 3 人,既学舞蹈又学声乐的有 2 人,从该兴趣小组中任选 2 人,设$X$为选出的既学舞蹈又学声乐的人数.若$P(X > 0) = \frac{11}{21}$,则该兴趣小组的人数是
7
.
答案:
10.7
11. (2025·吉林阶段练习)门卫室有 5 把钥匙,其中只有一把能打开办公室的门,由于借钥匙开门的员工不知哪把是开门的钥匙,他只好逐一尝试.若不能开门,则标记后换一把钥匙继续尝试开门,记打开门时,试开门的次数为$X$.求:
(1)$X$的分布列;
(2)该员工至多试开 3 次的概率.
(1)$X$的分布列;
(2)该员工至多试开 3 次的概率.
答案:
11.解:
(1)X的可能取值为1,2,3,4,5,则P(X=1)=$\frac{1}{5}$,P(X=2)=$\frac{4}{5}×\frac{1}{4}$=$\frac{1}{5}$,P(X=3)=$\frac{4}{5}×\frac{3}{4}×\frac{1}{3}$=$\frac{1}{5}$,P(X=4)=$\frac{4}{5}×\frac{3}{4}×\frac{2}{3}×\frac{1}{2}$=$\frac{1}{5}$,P(X=5)=$\frac{4}{5}×\frac{3}{4}×\frac{2}{3}×\frac{1}{2}×1$=$\frac{1}{5}$.因此X的分布列为
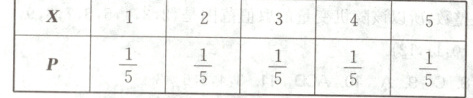
(2)P(X$\leq$3)=P(X=1)+P(X=2)+P(X=3)=$\frac{1}{5}$+$\frac{1}{5}$+$\frac{1}{5}$=$\frac{3}{5}$,即该员工至多试开3次的概率是$\frac{3}{5}$.
11.解:
(1)X的可能取值为1,2,3,4,5,则P(X=1)=$\frac{1}{5}$,P(X=2)=$\frac{4}{5}×\frac{1}{4}$=$\frac{1}{5}$,P(X=3)=$\frac{4}{5}×\frac{3}{4}×\frac{1}{3}$=$\frac{1}{5}$,P(X=4)=$\frac{4}{5}×\frac{3}{4}×\frac{2}{3}×\frac{1}{2}$=$\frac{1}{5}$,P(X=5)=$\frac{4}{5}×\frac{3}{4}×\frac{2}{3}×\frac{1}{2}×1$=$\frac{1}{5}$.因此X的分布列为

(2)P(X$\leq$3)=P(X=1)+P(X=2)+P(X=3)=$\frac{1}{5}$+$\frac{1}{5}$+$\frac{1}{5}$=$\frac{3}{5}$,即该员工至多试开3次的概率是$\frac{3}{5}$.
12. 新定义 (多选题)(2025·新乡期中)已知$\min\{x_1,x_2,·s,x_n\}$表示$x_1,x_2,·s,x_n$中最小的数,$\max \{x_1,x_2,·s,x_n\}$表示$x_1,x_2,·s,x_n$中最大的数.若数列$\{a_n\}$,$\{b_n\}$都只有 8 项,且都是由数字 1,2,3,4,5,6,7,8随机排列而成的(每个数字都出现,但不重复出现),记$X = \min\{\max\{a_1,a_2,a_3,a_4\},\max\{a_5,a_6,a_7,a_8\}\}$,$Y = \max\{\min\{b_1,b_2,b_3,b_4\},\min\{b_5,b_6,b_7,b_8\}\}$,则下列说法正确的是
(
A.$X$的值可能为 4,5,6,7
B.$Y$的值可能为 3,4,5,6
C.$X \geq 6$的概率为$\frac{6}{7}$
D.$X > Y$的概率为$\frac{1 216}{1 225}$
(
ACD
)A.$X$的值可能为 4,5,6,7
B.$Y$的值可能为 3,4,5,6
C.$X \geq 6$的概率为$\frac{6}{7}$
D.$X > Y$的概率为$\frac{1 216}{1 225}$
答案:
12.ACD
13. (2025·河池阶段练习)某校运动会长跑比赛分为预赛、半决赛和决赛,只有预赛、半决赛都晋级才能进入决赛.已知高二(1)班在预赛和半决赛中晋级的概率分别为$\frac{2}{3}$和$\frac{2}{3}$;高二(2)班在预赛和半决赛中晋级的概率分别为$\frac{2}{3}$和$\frac{3}{4}$;高二(3)班在预赛和半决赛中晋级的概率分别为$\frac{3}{4}$和$\frac{4}{5}$.
(1) 高二(1)班、高二(2)班、高二(3)班中哪个班级进入决赛的概率最大?
(2) 设三个班级中进入决赛的班级数为$\xi$,求$\xi$的分布列.
(1) 高二(1)班、高二(2)班、高二(3)班中哪个班级进入决赛的概率最大?
(2) 设三个班级中进入决赛的班级数为$\xi$,求$\xi$的分布列.
答案:
13.解:
(1)由题意,得高二
(1)班进入决赛的概率为$\frac{2}{3}×\frac{2}{3}$=$\frac{4}{9}$,高二
(2)班进入决赛的概率为$\frac{2}{3}×\frac{3}{4}$=$\frac{1}{2}$,高二
(3)班进入决赛的概率为$\frac{3}{4}×\frac{4}{5}$=$\frac{3}{5}$.因为$\frac{3}{5}$>$\frac{1}{2}$>$\frac{4}{9}$,所以高二
(3)班进入决赛的概率最大。
(2)由
(1)可知,高二
(1)班、高二
(2)班、高二
(3)班进入决赛的概率分别为$\frac{4}{9}$,$\frac{1}{2}$,$\frac{3}{5}$,则$\xi$的可能取值为0,1,2,3.P($\xi$=0)=$(1 - \frac{4}{9})×(1 - \frac{1}{2})×(1 - \frac{3}{5})$=$\frac{1}{9}$,P($\xi$=1)=$(1 - \frac{4}{9})×(1 - \frac{1}{2})×\frac{3}{5}$+$(1 - \frac{4}{9})×\frac{1}{2}×(1 - \frac{3}{5})$+$\frac{4}{9}×(1 - \frac{1}{2})×(1 - \frac{3}{5})$=$\frac{11}{30}$,P($\xi$=2)=$(1 - \frac{4}{9})×\frac{1}{2}×\frac{3}{5}$+$\frac{4}{9}×(1 - \frac{1}{2})×\frac{3}{5}$+$\frac{4}{9}×\frac{1}{2}×(1 - \frac{3}{5})$=$\frac{7}{18}$,P($\xi$=3)=$\frac{4}{9}×\frac{1}{2}×\frac{3}{5}$=$\frac{2}{15}$,所以$\xi$的分布列为

13.解:
(1)由题意,得高二
(1)班进入决赛的概率为$\frac{2}{3}×\frac{2}{3}$=$\frac{4}{9}$,高二
(2)班进入决赛的概率为$\frac{2}{3}×\frac{3}{4}$=$\frac{1}{2}$,高二
(3)班进入决赛的概率为$\frac{3}{4}×\frac{4}{5}$=$\frac{3}{5}$.因为$\frac{3}{5}$>$\frac{1}{2}$>$\frac{4}{9}$,所以高二
(3)班进入决赛的概率最大。
(2)由
(1)可知,高二
(1)班、高二
(2)班、高二
(3)班进入决赛的概率分别为$\frac{4}{9}$,$\frac{1}{2}$,$\frac{3}{5}$,则$\xi$的可能取值为0,1,2,3.P($\xi$=0)=$(1 - \frac{4}{9})×(1 - \frac{1}{2})×(1 - \frac{3}{5})$=$\frac{1}{9}$,P($\xi$=1)=$(1 - \frac{4}{9})×(1 - \frac{1}{2})×\frac{3}{5}$+$(1 - \frac{4}{9})×\frac{1}{2}×(1 - \frac{3}{5})$+$\frac{4}{9}×(1 - \frac{1}{2})×(1 - \frac{3}{5})$=$\frac{11}{30}$,P($\xi$=2)=$(1 - \frac{4}{9})×\frac{1}{2}×\frac{3}{5}$+$\frac{4}{9}×(1 - \frac{1}{2})×\frac{3}{5}$+$\frac{4}{9}×\frac{1}{2}×(1 - \frac{3}{5})$=$\frac{7}{18}$,P($\xi$=3)=$\frac{4}{9}×\frac{1}{2}×\frac{3}{5}$=$\frac{2}{15}$,所以$\xi$的分布列为

查看更多完整答案,请扫码查看


