2025年通成学典课时作业本高中数学选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通成学典课时作业本高中数学选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列随机变量不服从两点分布的是 (
A.抛掷一枚质地均匀的骰子,所得点数为随机变量$X$
B.某射手射击一次,击中目标的次数为随机变量$X$
C.从装有 5 个红球、3 个白球的袋中取一个球,令随机变量$X = \begin{cases} 1, 取出白球 \\ 0, 取出红球 \end{cases}$
D.某医生做一次手术,手术成功的次数为随机变量$X$
A
)A.抛掷一枚质地均匀的骰子,所得点数为随机变量$X$
B.某射手射击一次,击中目标的次数为随机变量$X$
C.从装有 5 个红球、3 个白球的袋中取一个球,令随机变量$X = \begin{cases} 1, 取出白球 \\ 0, 取出红球 \end{cases}$
D.某医生做一次手术,手术成功的次数为随机变量$X$
答案:
1.A
2. (2025·蚌埠阶段练习)已知离散型随机变量$X$的分布列为$P(X = i) = \frac{1}{3}(i = 1,2,3)$,则$P(X \geq 2)$等于
(
A.$\frac{1}{6}$
B.$\frac{1}{3}$
C.$\frac{1}{2}$
D.$\frac{2}{3}$
(
D
)A.$\frac{1}{6}$
B.$\frac{1}{3}$
C.$\frac{1}{2}$
D.$\frac{2}{3}$
答案:
2.D
3. (多选题)下列表格中,不是某个随机变量的分布列的是 (
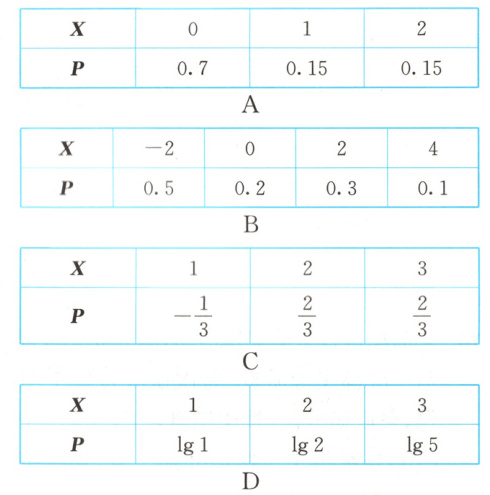
BC
)
答案:
3.BC
4. (多选题)设随机变量$\xi$的分布列为$P(\xi = \frac{k}{5}) = ak$,$k = 1,2,3,4,5$,下列结论正确的是(
A.$15a = 1$
B.$P(0.4 < \xi < 0.8) = 0.2$
C.$P(0.1 < \xi < 0.6) = 0.2$
D.$P(\xi = 1) = 0.3$
ABC
)A.$15a = 1$
B.$P(0.4 < \xi < 0.8) = 0.2$
C.$P(0.1 < \xi < 0.6) = 0.2$
D.$P(\xi = 1) = 0.3$
答案:
4.ABC
5. 已知随机变量$\eta$的分布列为

则$x =$

则$x =$
0
,$P(\eta \leq 3) =$0.55
.
答案:
5.0 0.55
6. 吃粽子是我国端午节的传统习俗.现有 10 个粽子,其中红豆粽 2 个,肉粽 3 个,蛋黄粽 5 个,假设这三种粽子除馅料外完全相同.从中任意选取 3 个.
(1) 求选取的 3 个粽子中恰有 1 个肉粽的概率;
(2) 设$\xi$表示取到的红豆粽个数,求$\xi$的分布列,并求事件“选取的 3 个粽子中红豆粽不少于 1 个”的概率.
(1) 求选取的 3 个粽子中恰有 1 个肉粽的概率;
(2) 设$\xi$表示取到的红豆粽个数,求$\xi$的分布列,并求事件“选取的 3 个粽子中红豆粽不少于 1 个”的概率.
答案:
6.解:
(1)设A=“选取的3个粽子中恰有1个肉粽”,则由古典概型的概率计算公式可知,P(A)=$\frac{C_{3}^{1}C_{7}^{2}}{C_{10}^{3}}$=$\frac{21}{40}$,所以选取的3个粽子中恰有1个肉粽的概率为$\frac{21}{40}$。
(2)由题意可知,$\xi$的所有可能取值为0,1,2.因为P($\xi$=k)=$\frac{C_{2}^{k}C_{8}^{3 - k}}{C_{10}^{3}}$,k=0,1,2,所以P($\xi$=0)=$\frac{C_{2}^{0}C_{8}^{3}}{C_{10}^{3}}$=$\frac{7}{15}$,P($\xi$=1)=$\frac{C_{2}^{1}C_{8}^{2}}{C_{10}^{3}}$=$\frac{7}{15}$,P($\xi$=2)=$\frac{C_{2}^{2}C_{8}^{1}}{C_{10}^{3}}$=$\frac{1}{15}$.所以$\xi$的分布列为
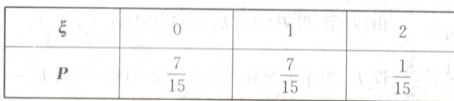
所以“选取的3个粽子中红豆粽不少于1个”的概率为P($\xi\geq1$)=P($\xi$=1)+P($\xi$=2)=$\frac{7}{15}$+$\frac{1}{15}$=$\frac{8}{15}$.
6.解:
(1)设A=“选取的3个粽子中恰有1个肉粽”,则由古典概型的概率计算公式可知,P(A)=$\frac{C_{3}^{1}C_{7}^{2}}{C_{10}^{3}}$=$\frac{21}{40}$,所以选取的3个粽子中恰有1个肉粽的概率为$\frac{21}{40}$。
(2)由题意可知,$\xi$的所有可能取值为0,1,2.因为P($\xi$=k)=$\frac{C_{2}^{k}C_{8}^{3 - k}}{C_{10}^{3}}$,k=0,1,2,所以P($\xi$=0)=$\frac{C_{2}^{0}C_{8}^{3}}{C_{10}^{3}}$=$\frac{7}{15}$,P($\xi$=1)=$\frac{C_{2}^{1}C_{8}^{2}}{C_{10}^{3}}$=$\frac{7}{15}$,P($\xi$=2)=$\frac{C_{2}^{2}C_{8}^{1}}{C_{10}^{3}}$=$\frac{1}{15}$.所以$\xi$的分布列为

所以“选取的3个粽子中红豆粽不少于1个”的概率为P($\xi\geq1$)=P($\xi$=1)+P($\xi$=2)=$\frac{7}{15}$+$\frac{1}{15}$=$\frac{8}{15}$.
7. (2024·邢台期末)已知随机变量$\xi$的分布列为

A.$\frac{1}{3}$
B.$\frac{1}{4}$
C.$\frac{1}{2}$
D.$\frac{2}{3}$

A.$\frac{1}{3}$
B.$\frac{1}{4}$
C.$\frac{1}{2}$
D.$\frac{2}{3}$
答案:
7.D
查看更多完整答案,请扫码查看


