2025年通成学典课时作业本高中数学选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通成学典课时作业本高中数学选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. (2025·齐齐哈尔期中)为调查居民对两会相关知识的了解情况,某小区开展了两会知识问答活动,现将该小区参与该活动的 800 名居民的得分(满分 100 分)进行了统计,得到如图所示的频率分布直方图.
(1)根据频率分布直方图,估计这 800 名居民得分数据的平均值 $\overline{x}$(同一组数据以该组区间的中点值作代表);
(2)结合频率分布直方图,近似认为参与活动的小区居民的得分数据 $X$ 服从正态分布 $N(\mu,81)$,其中 $\mu$ 近似为(1)中的样本平均值 $\overline{x}$,试估计得分超过 95.8 分的居民人数(结果精确到个位);
(3)用频率估计概率,任选 2 名参加活动的居民,设 $Y$ 为得分超过 80 分的居民人数,求 $Y$ 的分布列和数学期望.
附:若随机变量 $X$ 服从正态分布 $N(\mu,\sigma^{2})$,则 $P(\mu-\sigma\leqslant X\leqslant\mu+\sigma)\approx0.6827$,$P(\mu - 2\sigma\leqslant X\leqslant\mu + 2\sigma)\approx0.9545$,$P(\mu - 3\sigma\leqslant X\leqslant\mu + 3\sigma)\approx0.9973$.

(1)根据频率分布直方图,估计这 800 名居民得分数据的平均值 $\overline{x}$(同一组数据以该组区间的中点值作代表);
(2)结合频率分布直方图,近似认为参与活动的小区居民的得分数据 $X$ 服从正态分布 $N(\mu,81)$,其中 $\mu$ 近似为(1)中的样本平均值 $\overline{x}$,试估计得分超过 95.8 分的居民人数(结果精确到个位);
(3)用频率估计概率,任选 2 名参加活动的居民,设 $Y$ 为得分超过 80 分的居民人数,求 $Y$ 的分布列和数学期望.
附:若随机变量 $X$ 服从正态分布 $N(\mu,\sigma^{2})$,则 $P(\mu-\sigma\leqslant X\leqslant\mu+\sigma)\approx0.6827$,$P(\mu - 2\sigma\leqslant X\leqslant\mu + 2\sigma)\approx0.9545$,$P(\mu - 3\sigma\leqslant X\leqslant\mu + 3\sigma)\approx0.9973$.

答案:
1. 解:
(1) 由题意,得$\bar{x}=45×0.04+55×0.08+65×0.12+75×0.26+85×0.32+95×0.18=77.8$。
(2) 由
(1),得$X\sim N(77.8,9^{2})$,则$P(X>95.8)=P(X>\mu + 2\sigma)=\frac{1 - P(\mu - 2\sigma\leq X\leq\mu + 2\sigma)}{2}\approx0.02275$,所以估计得分超过$95.8$分的居民人数为$800×0.02275\approx18$。
(3) 用频率估计概率,从该小区任选$1$名居民,该居民得分超过$80$分的概率为$(0.032 + 0.018)×10 = 0.5$。所以该小区任选$2$名居民互不影响,则得分超过$80$分的居民人数$Y$可能的取值为$0$,$1$,$2$,且$Y\sim B(2,\frac{1}{2})$。所以$P(Y = k)=C_{2}^{k}×(\frac{1}{2})^{k}×(1 - \frac{1}{2})^{2 - k}$,$k = 0$,$1$,$2$,则$P(Y = 0)=C_{2}^{0}×(\frac{1}{2})^{2}=\frac{1}{4}$,$P(Y = 1)=C_{2}^{1}×\frac{1}{2}×\frac{1}{2}=\frac{1}{2}$,$P(Y = 2)=C_{2}^{2}×(\frac{1}{2})^{2}=\frac{1}{4}$。$Y$的分布列为
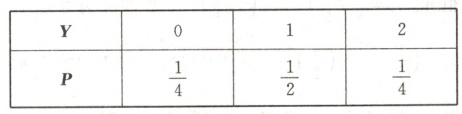
$E(Y)=0×\frac{1}{4}+1×\frac{1}{2}+2×\frac{1}{4}=1$。
1. 解:
(1) 由题意,得$\bar{x}=45×0.04+55×0.08+65×0.12+75×0.26+85×0.32+95×0.18=77.8$。
(2) 由
(1),得$X\sim N(77.8,9^{2})$,则$P(X>95.8)=P(X>\mu + 2\sigma)=\frac{1 - P(\mu - 2\sigma\leq X\leq\mu + 2\sigma)}{2}\approx0.02275$,所以估计得分超过$95.8$分的居民人数为$800×0.02275\approx18$。
(3) 用频率估计概率,从该小区任选$1$名居民,该居民得分超过$80$分的概率为$(0.032 + 0.018)×10 = 0.5$。所以该小区任选$2$名居民互不影响,则得分超过$80$分的居民人数$Y$可能的取值为$0$,$1$,$2$,且$Y\sim B(2,\frac{1}{2})$。所以$P(Y = k)=C_{2}^{k}×(\frac{1}{2})^{k}×(1 - \frac{1}{2})^{2 - k}$,$k = 0$,$1$,$2$,则$P(Y = 0)=C_{2}^{0}×(\frac{1}{2})^{2}=\frac{1}{4}$,$P(Y = 1)=C_{2}^{1}×\frac{1}{2}×\frac{1}{2}=\frac{1}{2}$,$P(Y = 2)=C_{2}^{2}×(\frac{1}{2})^{2}=\frac{1}{4}$。$Y$的分布列为

$E(Y)=0×\frac{1}{4}+1×\frac{1}{2}+2×\frac{1}{4}=1$。
2. (2025·哈尔滨阶段练习)某汽车销售公司为了提升业绩,将最近一段时间内每日的汽车销售情况进行了统计,绘制成如图所示的频率分布直方图.
(1)求 $a$ 的值,并估计该公司这段时间内每日汽车销售量的第 60 百分位数.
(2)以频率估计概率,若在这段时间内随机抽取 4 天,设每日汽车销售量(单位:辆)在 $[200,250)$ 内的天数为 $X$,在恰有 1 天的汽车销售量不超过 150 辆的条件下,求 $X$ 的分布列及数学期望.
(3)为增加销售量,公司规定顾客每购买一辆汽车可以进行一次抽奖活动,规则如下:在三棱锥 $A - BCD$ 中,$\triangle BCD$,$\triangle ACD$ 均是边长为 2 的正三角形,$AB = \sqrt{3}$. 现从写有数字 1~8 的八个标签中随机选择两个分别贴在 $A$,$B$ 两个顶点上,记顶点 $A$,$B$ 上的数字分别为 $m$ 和 $n$,若 $E$ 为侧棱 $AB$ 上一个动点,满足 $\frac{|AE|}{|EB|} = \frac{m}{n}$,“二面角 $E - CD - A$ 大于 $\frac{\pi}{4}$”即为中奖,求中奖的概率.

(1)求 $a$ 的值,并估计该公司这段时间内每日汽车销售量的第 60 百分位数.
(2)以频率估计概率,若在这段时间内随机抽取 4 天,设每日汽车销售量(单位:辆)在 $[200,250)$ 内的天数为 $X$,在恰有 1 天的汽车销售量不超过 150 辆的条件下,求 $X$ 的分布列及数学期望.
(3)为增加销售量,公司规定顾客每购买一辆汽车可以进行一次抽奖活动,规则如下:在三棱锥 $A - BCD$ 中,$\triangle BCD$,$\triangle ACD$ 均是边长为 2 的正三角形,$AB = \sqrt{3}$. 现从写有数字 1~8 的八个标签中随机选择两个分别贴在 $A$,$B$ 两个顶点上,记顶点 $A$,$B$ 上的数字分别为 $m$ 和 $n$,若 $E$ 为侧棱 $AB$ 上一个动点,满足 $\frac{|AE|}{|EB|} = \frac{m}{n}$,“二面角 $E - CD - A$ 大于 $\frac{\pi}{4}$”即为中奖,求中奖的概率.

答案:
2. 解:
(1) 由$(0.001 + 0.002 + 0.003 + 2a + 0.006)×50 = 1$,得$a = 0.004$。因为$(0.002 + 0.003 + 0.004)×50 = 0.45$,$(0.002 + 0.003 + 0.004 + 0.006)×50 = 0.75$,所以每日汽车销售量(单位:辆)的第$60$百分位数在$[150,200)$内,且约为$150+\frac{0.6 - 0.45}{0.75 - 0.45}×50 = 175$。
(2) 因为抽取的$1$天汽车销售量不超过$150$辆的概率为$0.45$,抽取的$1$天汽车销售量(单位:辆)在$[200,250)$内的概率为$0.2$,所以在恰有$1$天的汽车销售量不超过$150$辆的条件下,抽取的$1$天汽车销售量(单位:辆)在$[200,250)$内的概率为$p=\frac{0.2}{1 - 0.45}=\frac{4}{11}$。由题意,得$X$的值可以为$0$,$1$,$2$,$3$,则$P(X = 0)=C_{3}^{0}×(\frac{7}{11})^{3}=\frac{343}{1331}$,$P(X = 1)=C_{3}^{1}×\frac{4}{11}×(\frac{7}{11})^{2}=\frac{588}{1331}$,$P(X = 2)=C_{3}^{2}×(\frac{4}{11})^{2}×\frac{7}{11}=\frac{336}{1331}$,$P(X = 3)=C_{3}^{3}×(\frac{4}{11})^{3}=\frac{64}{1331}$。所以$X$的分布列为
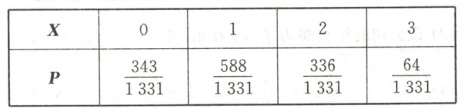
所以$E(X)=3×\frac{4}{11}=\frac{12}{11}$。
(3) 如图,取$CD$的中点$F$,连接$BF$,$EF$,$AF$,$CE$,$DE$。因为$\triangle BCD$,$\triangle ACD$都是边长为$2$的等边三角形,所以$CD\perp BF$,$CD\perp AF$。又$BF$,$AF\subset$平面$ABF$,$BF\cap AF = F$,所以$CD\perp$平面$ABF$。因为$EF\subset$平面$ABF$,所以$CD\perp EF$。所以易得$\angle EFA$为二面角$E - CD - A$的平面角。在$\triangle ABF$中,易得$AB = BF = AF=\sqrt{3}$,所以$\angle BFA=\frac{\pi}{3}$。若$\angle EFA=\frac{\pi}{4}$,在$\triangle AEF$中,由正弦定理,得$\frac{m}{\sin\frac{\pi}{4}}=\frac{\sqrt{3}}{\sin\frac{5\pi}{12}}$,则$m=\frac{\sqrt{3}\sin\frac{\pi}{4}}{\sin\frac{5\pi}{12}}=\sqrt{3}-1$,此时$n=\sqrt{3}-(\sqrt{3}-1)=1$,则$\frac{m}{n}=\sqrt{3}+1$。所以要想中奖,须有$\frac{m}{n}>\sqrt{3}+1$。由$m$,$n$是从数字$1\sim8$中随机选择的两个,所以基本事件有$A_{8}^{2}=56$(个),满足$\frac{m}{n}>\sqrt{3}+1$的基本事件$(m,n)$有$(8,1)$,$(8,2)$,$(7,1)$,$(7,2)$,$(6,1)$,$(6,2)$,$(5,1)$,$(4,1)$,$(3,1)$,共$9$个。所以中奖的概率为$\frac{9}{56}$。

2. 解:
(1) 由$(0.001 + 0.002 + 0.003 + 2a + 0.006)×50 = 1$,得$a = 0.004$。因为$(0.002 + 0.003 + 0.004)×50 = 0.45$,$(0.002 + 0.003 + 0.004 + 0.006)×50 = 0.75$,所以每日汽车销售量(单位:辆)的第$60$百分位数在$[150,200)$内,且约为$150+\frac{0.6 - 0.45}{0.75 - 0.45}×50 = 175$。
(2) 因为抽取的$1$天汽车销售量不超过$150$辆的概率为$0.45$,抽取的$1$天汽车销售量(单位:辆)在$[200,250)$内的概率为$0.2$,所以在恰有$1$天的汽车销售量不超过$150$辆的条件下,抽取的$1$天汽车销售量(单位:辆)在$[200,250)$内的概率为$p=\frac{0.2}{1 - 0.45}=\frac{4}{11}$。由题意,得$X$的值可以为$0$,$1$,$2$,$3$,则$P(X = 0)=C_{3}^{0}×(\frac{7}{11})^{3}=\frac{343}{1331}$,$P(X = 1)=C_{3}^{1}×\frac{4}{11}×(\frac{7}{11})^{2}=\frac{588}{1331}$,$P(X = 2)=C_{3}^{2}×(\frac{4}{11})^{2}×\frac{7}{11}=\frac{336}{1331}$,$P(X = 3)=C_{3}^{3}×(\frac{4}{11})^{3}=\frac{64}{1331}$。所以$X$的分布列为

所以$E(X)=3×\frac{4}{11}=\frac{12}{11}$。
(3) 如图,取$CD$的中点$F$,连接$BF$,$EF$,$AF$,$CE$,$DE$。因为$\triangle BCD$,$\triangle ACD$都是边长为$2$的等边三角形,所以$CD\perp BF$,$CD\perp AF$。又$BF$,$AF\subset$平面$ABF$,$BF\cap AF = F$,所以$CD\perp$平面$ABF$。因为$EF\subset$平面$ABF$,所以$CD\perp EF$。所以易得$\angle EFA$为二面角$E - CD - A$的平面角。在$\triangle ABF$中,易得$AB = BF = AF=\sqrt{3}$,所以$\angle BFA=\frac{\pi}{3}$。若$\angle EFA=\frac{\pi}{4}$,在$\triangle AEF$中,由正弦定理,得$\frac{m}{\sin\frac{\pi}{4}}=\frac{\sqrt{3}}{\sin\frac{5\pi}{12}}$,则$m=\frac{\sqrt{3}\sin\frac{\pi}{4}}{\sin\frac{5\pi}{12}}=\sqrt{3}-1$,此时$n=\sqrt{3}-(\sqrt{3}-1)=1$,则$\frac{m}{n}=\sqrt{3}+1$。所以要想中奖,须有$\frac{m}{n}>\sqrt{3}+1$。由$m$,$n$是从数字$1\sim8$中随机选择的两个,所以基本事件有$A_{8}^{2}=56$(个),满足$\frac{m}{n}>\sqrt{3}+1$的基本事件$(m,n)$有$(8,1)$,$(8,2)$,$(7,1)$,$(7,2)$,$(6,1)$,$(6,2)$,$(5,1)$,$(4,1)$,$(3,1)$,共$9$个。所以中奖的概率为$\frac{9}{56}$。

查看更多完整答案,请扫码查看


