2025年大联考单元期末测试卷七年级数学上册沪科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年大联考单元期末测试卷七年级数学上册沪科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
15. 计算:$-2^{2}÷\frac{4}{3}-\frac{1}{3}×[(-3)^{2}-2]+|-2|÷\frac{1}{5}$.
答案:
15.解:原式=-4×$\frac{3}{4}$-$\frac{1}{3}$×(9 - 2)+2÷$\frac{1}{5}$(4分)
=-3-$\frac{7}{3}$+10
=$\frac{14}{3}$.(8分)
=-3-$\frac{7}{3}$+10
=$\frac{14}{3}$.(8分)
16. 解方程:$\frac{1 - 2x}{7}-1=\frac{x + 3}{3}$.
答案:
16.解:去分母,得3(1 - 2x)-21 = 7(x + 3),(2分)
去括号,得3 - 6x - 21 = 7x + 21,(4分)
移项,得-6x - 7x = 21 - 3 + 21,(6分)
合并同类项,得-13x = 39,
两边同除以-13,得x = -3.(8分)
去括号,得3 - 6x - 21 = 7x + 21,(4分)
移项,得-6x - 7x = 21 - 3 + 21,(6分)
合并同类项,得-13x = 39,
两边同除以-13,得x = -3.(8分)
17. 已知$A = (2x^{2}+xy - 5)-2(2xy + x^{2}-1)$.
(1)化简A.
(2)若$x = -2$,$y = 3$,求A的值.
(1)化简A.
(2)若$x = -2$,$y = 3$,求A的值.
答案:
17.解:
(1)A=(2x²+xy - 5)-2(2xy+x²-1)
=-3xy - 3.(4分)
(2)当x = -2,y = 3时,
A=-3xy - 3=-3×(-2)×3 - 3 = 15.(8分)
(1)A=(2x²+xy - 5)-2(2xy+x²-1)
=-3xy - 3.(4分)
(2)当x = -2,y = 3时,
A=-3xy - 3=-3×(-2)×3 - 3 = 15.(8分)
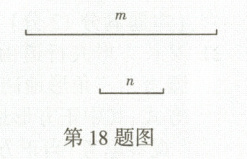
18. 已知线段m,n(其中$m > n$).
(1)尺规作图:作线段$AC = m - n$,其中$AB = m$,$BC = n$(不写作法,保留作图痕迹).
(2)在(1)的条件下,点M是AB的中点,点N是BC的中点,当$m = 3$,$n = 1$时,求线段MN的长.
(1)尺规作图:作线段$AC = m - n$,其中$AB = m$,$BC = n$(不写作法,保留作图痕迹).
(2)在(1)的条件下,点M是AB的中点,点N是BC的中点,当$m = 3$,$n = 1$时,求线段MN的长.

答案:
18.解:
(1)如图所示,线段AC即为所求.(4分)
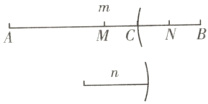
(2)因为点M是AB的中点,所以AM = BM=$\frac{1}{2}$AB.
因为点N是BC的中点,所以CN = BN=$\frac{1}{2}$BC.(6分)
当m = 3,n = 1时,BM=$\frac{1}{2}$×3=$\frac{3}{2}$,BN=$\frac{1}{2}$×1=$\frac{1}{2}$,
所以MN = BM - BN=$\frac{3}{2}$-$\frac{1}{2}$=1.(8分)
18.解:
(1)如图所示,线段AC即为所求.(4分)
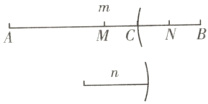
(2)因为点M是AB的中点,所以AM = BM=$\frac{1}{2}$AB.
因为点N是BC的中点,所以CN = BN=$\frac{1}{2}$BC.(6分)
当m = 3,n = 1时,BM=$\frac{1}{2}$×3=$\frac{3}{2}$,BN=$\frac{1}{2}$×1=$\frac{1}{2}$,
所以MN = BM - BN=$\frac{3}{2}$-$\frac{1}{2}$=1.(8分)
查看更多完整答案,请扫码查看


