《2025年大联考单元期末测试卷七年级数学上册沪科版》

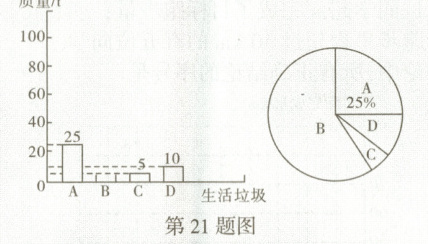
21. 生活垃圾的分类与回收利用可以减少污染,生活垃圾一般可分为四大类:可回收物(A)、厨余垃圾(B)、有害垃圾(C)和其他垃圾(D),某垃圾处理厂统计了居民的生活垃圾的分类情况,以下是根据调查结果分别整理的不完整的条形统计图和扇形统计图.
请你根据上述统计图提供的信息,回答下列问题.
(1) 求在此次调查中,表示“其他垃圾(D)”部分的扇形的圆心角的度数.
(2) 请补全条形统计图.
(3) 研究发现,在可回收物(A)中废纸约占15%,某企业利用回收的1 t废纸可生产0.8 t新纸,若该市每天生活垃圾为4 000 t,则该企业每天利用回收的废纸可以生产多少吨新纸?

答案：
21. 解：
(1)本次调查的垃圾的总数量为$25÷25\% = 100$ (t),
表示“其他垃圾(D)”部分的扇形的圆心角的度数为$360^{\circ}×\frac{10}{100} = 36^{\circ}$.(4分)
(2)厨余垃圾B的质量为$100 - 25 - 5 - 10 = 60$ (t)，补全条形统计图如图所示.
(8分)
(3)$4000×\frac{25}{100}×15\%×0.8 = 1000×15\%×0.8 = 120$ (t).
答：该企业每天利用回收的废纸可以生产120t新纸.(12分)

22. 观察下列两个等式$1 - \frac{2}{3} = 2×1×\frac{2}{3} - 1$,$2 - \frac{3}{5} = 2×2×\frac{3}{5} - 1$,给出定义如下:我们称使等式$a - b = 2ab - 1$成立的一对有理数$a$,$b$为“同心有理数对”,记为$(a,b)$. 例如:数对$(1,\frac{2}{3})$,$(2,\frac{3}{5})$,都是“同心有理数对”.
(1) 数对$(-2,1)$和$(3,\frac{4}{7})$是“同心有理数对”的为(3,$\frac{4}{7}$).
(2) 若$(a,3)$是“同心有理数对”,求$a$的值.
(3) 试说明:若$(m,n)$是“同心有理数对”,则$(-n,-m)$是“同心有理数对”.

答案： 22. 解：
(1)因为$-2 - 1 = -3$,$2×(-2)×1 - 1 = -5$,$-3≠ -5$,
所以数对$(-2,1)$不是“同心有理数对”;(2分)
因为$3 - \frac{4}{7} = \frac{17}{7}$,$2×3×\frac{4}{7} - 1 = \frac{17}{7}$,
所以$3 - \frac{4}{7} = 2×3×\frac{4}{7} - 1$,所以$(3,\frac{4}{7})$是“同心有理数对”，
所以数对$(-2,1)$和$(3,\frac{4}{7})$是“同心有理数对”的为$(3,\frac{4}{7})$.(4分)
(2)因为$(a,3)$是“同心有理数对”，
所以$a - 3 = 6a - 1$,所以$a = -\frac{2}{5}$.(8分)
(3)因为$(m,n)$是“同心有理数对”,所以$m - n = 2mn - 1$.
又因为$-n - (-m) = -n + m = m - n = 2mn - 1 = 2×(-n)×(-m) - 1$,
所以$(-n,-m)$是“同心有理数对”.(12分)