2025年大联考单元期末测试卷七年级数学上册沪科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年大联考单元期末测试卷七年级数学上册沪科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
7. 九月开学季,书店开展优惠活动,某套名著原价为 $m$ 元,现售价为 $(0.7m - 10)$ 元,则下列说法符合题意的是(
A.原价减10元后再打七折
B.原价打七折后再减10元
C.原价打三折后再减10元
D.原价减10元后再打三折
B
)A.原价减10元后再打七折
B.原价打七折后再减10元
C.原价打三折后再减10元
D.原价减10元后再打三折
答案:
7.B
8. 若 $x^{\vert n\vert + 1}y^{2}+(n + 2)x^{5}$ 是关于 $x,y$ 的五次二项式,则整数 $n$ 的值有(
A.2个
B.3个
C.4个
D.5个
C
)A.2个
B.3个
C.4个
D.5个
答案:
8.C
9. 教材变式·P87复习题T5一个三位数,百位上的数字为 $x$,十位上的数字比百位上的数字少3,个位上的数字是百位上的数字的2倍,这个三位数用含有 $x$ 的代数式表示为(
A.$112x - 30$
B.$100x - 30$
C.$112x + 30$
D.$102x + 30$
A
)A.$112x - 30$
B.$100x - 30$
C.$112x + 30$
D.$102x + 30$
答案:
9.A
10. 跨学科·信息技术有一数值转换器,原理如图所示. 若开始输入的 $x$ 的值是5,可发现第一次输出的结果是8,第二次输出的结果是4……则第2025次输出的结果是(
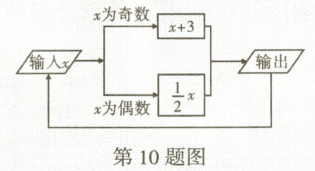
A.1
B.2
C.4
D.8
B
)
A.1
B.2
C.4
D.8
答案:
10.B
11. 把多项式 $3x - 2 + x^{2}+4x^{3}$ 按 $x$ 的降幂排列:
4x^{3}+x^{2}+3x - 2
.
答案:
11.$4x^{3}+x^{2}+3x - 2$
12. 多项式 $a^{2}+b^{2}$ 与 $a^{2}-b^{2}$ 的差是
2b^{2}
.
答案:
12.$2b^{2}$
13. 如图,下面每个格中的四个数都是按相同规律填写的,根据此规律,$x$ 的值为
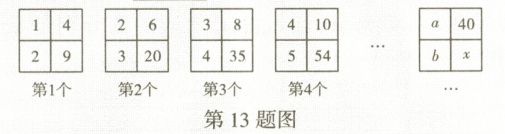
819
.
答案:
13.819
14. 若 $a + b = 2$,则称 $a$ 与 $b$ 是关于2的平衡数. 例如:$-5 + 7 = 2$. 所以 $-5$ 与7是关于2的平衡数,$11 + (-9)=2$,所以11与 $-9$ 是关于2的平衡数.
(1)3与
(2)若 $a = x^{2}-2(x^{2}-2x - 1)+1$,$a$ 与 $b$ 是关于2的平衡数,则 $b =$
(1)3与
-1
是关于2的平衡数.(2)若 $a = x^{2}-2(x^{2}-2x - 1)+1$,$a$ 与 $b$ 是关于2的平衡数,则 $b =$
x^{2}-4x - 1
(用含 $x$ 的代数式表示).
答案:
14.
(1)-1
(2)$x^{2}-4x - 1$
(1)-1
(2)$x^{2}-4x - 1$
15. 化简:
(1)$x^{2}-5xy + yx + 2x^{2}$.
(2)$2(3ab - 2c)-3(2ab - 5a)$.
(1)$x^{2}-5xy + yx + 2x^{2}$.
(2)$2(3ab - 2c)-3(2ab - 5a)$.
答案:
15.解:
(1)原式=$x^{2}+2x^{2}-5xy + xy$
=$3x^{2}-4xy$.(4分)
(2)原式=$6ab - 4c - 6ab + 15a$
=$15a - 4c$.(8分)
(1)原式=$x^{2}+2x^{2}-5xy + xy$
=$3x^{2}-4xy$.(4分)
(2)原式=$6ab - 4c - 6ab + 15a$
=$15a - 4c$.(8分)
查看更多完整答案,请扫码查看


