2026年学易优高考二轮总复习物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年学易优高考二轮总复习物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第80页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
[例 1] (2025·山东卷)在光电效应实验中,用频率和强度都相同的单色光分别照射编号为 1、2、3 的金属,所得遏止电压如图所示,关于光电子最大初动能 $ E_{k} $ 的大小关系正确的是 (

A.$ E_{k1} > E_{k2} > E_{k3} $
B.$ E_{k2} > E_{k3} > E_{k1} $
C.$ E_{k3} > E_{k2} > E_{k1} $
D.$ E_{k3} > E_{k1} > E_{k2} $
B
)
A.$ E_{k1} > E_{k2} > E_{k3} $
B.$ E_{k2} > E_{k3} > E_{k1} $
C.$ E_{k3} > E_{k2} > E_{k1} $
D.$ E_{k3} > E_{k1} > E_{k2} $
答案:
例1 答案:B
解析:根据光电子最大初动能与遏制电压的关系$E_{\mathrm{k}}=eU_{\mathrm{c}}$,根据图像有$U_{c2}>U_{c3}>U_{c1}$,故$E_{\mathrm{k}2}>E_{\mathrm{k}3}>E_{\mathrm{k}1}$,故B正确。
解析:根据光电子最大初动能与遏制电压的关系$E_{\mathrm{k}}=eU_{\mathrm{c}}$,根据图像有$U_{c2}>U_{c3}>U_{c1}$,故$E_{\mathrm{k}2}>E_{\mathrm{k}3}>E_{\mathrm{k}1}$,故B正确。
[例 2] (2025·山东济南一模)用不同波长的光照射光电管阴极探究光电效应的规律时,根据光电管的遏止电压 $ U_{c} $ 与对应入射光的波长 $ \lambda $ 作出的 $ U_{c} - \frac{1}{\lambda} $ 图像如图所示。已知光电子的电荷量大小为 $ e $,光速为 $ c $,下列说法正确的是 (
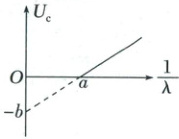
A.该光电管阴极材料的截止频率大小为 $ \frac{a}{c} $
B.由图像可得普朗克常量 $ h = \frac{ae}{bc} $
C.当用波长 $ \lambda = \frac{1}{3a} $ 的光照射光电管阴极时,光电子的最大初动能为 $ 2be $
D.当用波长 $ \lambda = \frac{1}{a} $ 的光照射光电管的阴极时,光电子的最大初动能随 $ \lambda $ 的增大而增大
C
)
A.该光电管阴极材料的截止频率大小为 $ \frac{a}{c} $
B.由图像可得普朗克常量 $ h = \frac{ae}{bc} $
C.当用波长 $ \lambda = \frac{1}{3a} $ 的光照射光电管阴极时,光电子的最大初动能为 $ 2be $
D.当用波长 $ \lambda = \frac{1}{a} $ 的光照射光电管的阴极时,光电子的最大初动能随 $ \lambda $ 的增大而增大
答案:
例2 答案:C
解析:根据动能定理$eU_{\mathrm{c}}=E_{\mathrm{k}m}$,又光电效应方程为$h\frac{c}{\lambda}=h\nu_{0} +E_{\mathrm{k}m}$,整理得$U_{\mathrm{c}}=\frac{hc}{e}·\frac{1}{\lambda}-\frac{h\nu_{0}}{e}$得$\frac{b}{a}=\frac{hc}{e}$,$-b=-\frac{h\nu_{0}}{e}$,普朗克常量为$h=\frac{be}{ac}$,该光电管阴极材料的截止频率大小为$\nu_{0} =ac$,故A、B错误;$\frac{1}{2}mv_{m}^{2}=h\nu -W_{0}=\frac{hc}{\lambda}-W_{0}$,将波长$\lambda=\frac{1}{3a}$代入光电效应方程,光电子的最大初动能为$E_{\mathrm{k}m}=2be$,故C正确;波长越长,光子能量越小,光电子的最大初动能随$\lambda$的增大而减小,故D错误。
解析:根据动能定理$eU_{\mathrm{c}}=E_{\mathrm{k}m}$,又光电效应方程为$h\frac{c}{\lambda}=h\nu_{0} +E_{\mathrm{k}m}$,整理得$U_{\mathrm{c}}=\frac{hc}{e}·\frac{1}{\lambda}-\frac{h\nu_{0}}{e}$得$\frac{b}{a}=\frac{hc}{e}$,$-b=-\frac{h\nu_{0}}{e}$,普朗克常量为$h=\frac{be}{ac}$,该光电管阴极材料的截止频率大小为$\nu_{0} =ac$,故A、B错误;$\frac{1}{2}mv_{m}^{2}=h\nu -W_{0}=\frac{hc}{\lambda}-W_{0}$,将波长$\lambda=\frac{1}{3a}$代入光电效应方程,光电子的最大初动能为$E_{\mathrm{k}m}=2be$,故C正确;波长越长,光子能量越小,光电子的最大初动能随$\lambda$的增大而减小,故D错误。
[例 3] (多选)(2025·浙江卷)如图 1 所示,三束由氢原子发出的可见光 $ P、Q、R $ 分别由真空玻璃管的窗口射向阴极 $ K $。调节滑动变阻器,记录电流表与电压表示数,两者关系如图 2 所示。下列说法正确的是 (

A.分别射入同一单缝衍射装置时,$ Q $ 的中央亮纹比 $ R $ 的宽
B.$ P、Q $ 产生的光电子在 $ K $ 处的最小德布罗意波长,$ P $ 大于 $ Q $
C.氢原子向第一激发态跃迁发光时,三束光中 $ Q $ 对应的能级最高
D.对应于图 2 中的 $ M $ 点,单位时间到达阳极 $ A $ 的光电子数目,$ P $ 多于 $ Q $

BC
)
A.分别射入同一单缝衍射装置时,$ Q $ 的中央亮纹比 $ R $ 的宽
B.$ P、Q $ 产生的光电子在 $ K $ 处的最小德布罗意波长,$ P $ 大于 $ Q $
C.氢原子向第一激发态跃迁发光时,三束光中 $ Q $ 对应的能级最高
D.对应于图 2 中的 $ M $ 点,单位时间到达阳极 $ A $ 的光电子数目,$ P $ 多于 $ Q $

答案:
例3 答案:BC
解析:由爱因斯坦光电效应方程得$E_{\mathrm{k}m}=h\nu -W_{0}$,又由动能定理得$-eU_{\mathrm{c}}=0 -E_{\mathrm{k}m}$,整理得$eU_{\mathrm{c}}=h\nu -W_{0}$,由题图2可知,$Q$的截止电压大于$R$的,则$Q$的频率大于$R$的频率,由$c=\lambda\nu$可知,$Q$的波长小于$R$的波长,则分别射入同一单缝衍射装置时,$Q$的中央亮纹比$R$的窄,故A错误;同理,$Q$产生的光电子的最大初动能比$P$的大,由德布罗意波长公式$\lambda=\frac{h}{p}$和$p=\sqrt{2mE_{\mathrm{k}m}}$得$\lambda=\frac{h}{\sqrt{2mE_{\mathrm{k}m}}}$,显然$P$产生的光电子在$K$处的最小德布罗意波长大于$Q$的,故B正确;结合A项分析,根据题图2可知$Q$的频率最大,由公式$E =h\nu$可知$Q$的光子能量最大,则由能级跃迁的频率条件$h\nu=E_{n}-E_{m}$可知,氢原子向第一激发态跃迁发光时,三束光中$Q$对应的能级最高,故C正确;对应于题图2中的$M$点,$P$和$Q$的光电流相等,则单位时间到达阳极$A$的光电子数目相等,故D错误。
解析:由爱因斯坦光电效应方程得$E_{\mathrm{k}m}=h\nu -W_{0}$,又由动能定理得$-eU_{\mathrm{c}}=0 -E_{\mathrm{k}m}$,整理得$eU_{\mathrm{c}}=h\nu -W_{0}$,由题图2可知,$Q$的截止电压大于$R$的,则$Q$的频率大于$R$的频率,由$c=\lambda\nu$可知,$Q$的波长小于$R$的波长,则分别射入同一单缝衍射装置时,$Q$的中央亮纹比$R$的窄,故A错误;同理,$Q$产生的光电子的最大初动能比$P$的大,由德布罗意波长公式$\lambda=\frac{h}{p}$和$p=\sqrt{2mE_{\mathrm{k}m}}$得$\lambda=\frac{h}{\sqrt{2mE_{\mathrm{k}m}}}$,显然$P$产生的光电子在$K$处的最小德布罗意波长大于$Q$的,故B正确;结合A项分析,根据题图2可知$Q$的频率最大,由公式$E =h\nu$可知$Q$的光子能量最大,则由能级跃迁的频率条件$h\nu=E_{n}-E_{m}$可知,氢原子向第一激发态跃迁发光时,三束光中$Q$对应的能级最高,故C正确;对应于题图2中的$M$点,$P$和$Q$的光电流相等,则单位时间到达阳极$A$的光电子数目相等,故D错误。
查看更多完整答案,请扫码查看


