《2026年学易优高考二轮总复习物理》

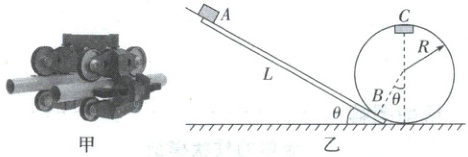
1. (2025·河南·一模)目前常见的过山车为了增加安全性，都用由上、下、侧三组轮子组成的安全装置把轨道车套在轨道上(如图甲)。现有与水平面成θ = 37°角的斜轨道和半径R = 10 m的光滑圆轨道相切于B点，且固定于竖直平面内，圆轨道的最低点位于地面(如图乙)。带安全装置、可视为质点的轨道车从斜面上的A点由静止释放，经B点后沿圆轨道运动、恰好到达最高点C，已知轨道车与斜轨道间的动摩擦因数μ = 0.25，重力加速度g取10 m/s²，sin 37° = 0.6，cos 37° = 0.8，则下列说法正确的是(C)


A.轨道车在C点的速度为10 m/s
B.轨道车在B点的速度为20 m/s
C.斜轨道A、B间的长度L为45 m
D.轨道车在C点受轨道的作用力一定向下

答案： 1.答案:C
解析:由于轨道车恰好经过最高点C，则轨道车到达最高点时速度为0，故A错误;轨道车由B到C的过程，根据机械能守恒定律可得$- mgR(1 + \cos\theta) = 0 - \frac{1}{2}mv_{B}^2$，解得$v_B = 6\sqrt{10} m/s$，故B错误;轨道车由A运动到B的过程中，由动能定理可得$mgL\sin\theta - \mu mgL\cos\theta = \frac{1}{2}mv_{B}^2$，解得$L = 45 m$，故C正确;轨道车在C点受轨道的向上作用力，故D错误。

2. (多选)(2025·陕西商洛·三模)如图所示，倾角为53°的光滑斜面固定在水平面上，轻质弹簧(劲度系数未知)一端悬挂在O点，另一端与质量为m的小球(视为质点)相连，B点在O点的正下方。小球从斜面上的A点由静止释放，沿着斜面下滑，已知OA与斜面垂直，且O、A两点间的距离为L，重力加速度大小为g，小球刚到达B点时，对斜面的弹力刚好为0，弹簧的原长为L，且始终处于弹性限度内，劲度系数为k的轻质弹簧的弹性势能$E_p$与弹簧的形变量x的关系为$E_p = \frac{1}{2}kx^2$，sin 53° = 0.8，cos 53° = 0.6，下列说法正确的是(BD)


A.弹簧的劲度系数为$\frac{mg}{3L}$
B.小球在B点时弹簧的弹性势能为$\frac{mgL}{3}$
C.小球到达B点时的动能为$\frac{6}{5}mgL$
D.小球从A点运动到B点的过程中，弹簧的弹性势能一直增大

答案： 2.答案:BD
解析:由几何关系可知$OB = \frac{5L}{3}$，又因为小球刚到达B点时与斜面间的弹力刚好为0，则有$k(\frac{5L}{3} - L) = mg$，解得$k = \frac{3mg}{2L}$，选项A错误;弹簧的弹性势能$E_{pB} = \frac{1}{2}k(\frac{2L}{3})^2 = \frac{mgL}{3}$，选项B正确;小球从A点运动到B点，弹簧的伸长量一直增大，弹簧的弹性势能一直增大，由能量守恒定律有$mg × \frac{4L}{3}\sin 53° = E_{pB} + E_k$，解得$E_k = \frac{11mgL}{15}$，选项C错误，D正确。故选BD。

[例 1] (多选)(2025·广东江门一模)数据表明，在电动车事故中，佩戴头盔可防止$85\%$的头部受伤，大大减小损伤程度。头盔内部的缓冲层与头部的撞击时间延长至$6\,ms$以上，人头部的质量约为$2\,kg$，则下列说法正确的是(ACD)


A.头盔减小了驾驶员头部撞击过程中的动量变化率
B.头盔减少了驾驶员头部撞击过程中撞击力的冲量
C.事故中头盔对头部的冲量与头部对头盔的冲量大小相等
D.若事故中头部以$6\,m/s$的速度水平撞击缓冲层，则头部受到的撞击力最多为$2000\,N$

答案： 例1 答案：ACD
解析：根据$F\Delta t=\Delta p$可得$F=\frac{\Delta p}{\Delta t}$，依题意知，头盔内部的缓冲层与头部的撞击时间延长了，头盔减小了驾驶员头部撞击过程中的动量变化率，故A正确；头盔并没有减少驾驶员头部撞击过程中撞击力的冲量，故B错误；根据$I=F\Delta t$知，头盔对头部的作用力与头部对头盔的作用力等大反向，作用时间相同，所以事故中头盔对头部的冲量与头部对头盔的冲量大小相等，故C正确；若事故中头部以$6\ m/s$的速度水平撞击缓冲层，则头部受到的撞击力$F=\frac{\Delta p}{\Delta t}=\frac{2×6}{6×10^{-3}}\ N=2000\ N$，即最多为$2000\ N$，故D正确。