《2026年学易优高考二轮总复习物理》

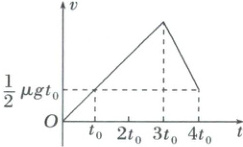
[例 1](多选)(2024·黑吉辽卷)一足够长木板置于水平地面上，二者间的动摩擦因数为$\mu$。$t = 0$时，木板在水平恒力作用下，由静止开始向右运动。某时刻，一小物块以与木板等大、反向的速度从右端滑上木板。已知$t = 0$到$t = 4t_{0}$的时间内，木板速度$v$随时间$t$变化的图像如图所示，其中$g$为重力加速度大小。$t = 4t_{0}$时刻，小物块和木板的速度相同。下列说法正确的是(ABD)


A.小物块在$t = 3t_{0}$时刻滑上木板
B.小物块和木板间的动摩擦因数为$2\mu$
C.小物块与木板的质量之比为$3:4$
D.$t = 4t_{0}$之后小物块和木板一起做匀速运动

答案： 例1 答案：ABD
解析：由$v-t$图像可知，在$3t_0$时刻木板的加速度发生变化，可知小物块在$t=3t_0$时刻滑上木板，A正确；由$v-t$图像可知，$0\sim3t_0$时间内，木板的加速度大小$a_1=\frac{1}{2}\mu g$，设木板的质量为$M$，对木板由牛顿第二定律有$F-\mu Mg=Ma_1$，解得$F=\frac{3}{2}\mu Mg$，在$t=3t_0$时，木板的速度$v_1=a_1·3t_0=\frac{3}{2}\mu gt_0$，根据题意可知$t=3t_0$时小物块以$\frac{3}{2}\mu gt_0$的速度水平向左滑上木板，$3t_0\sim4t_0$时间内，小物块的加速度大小$a'=\frac{\frac{1}{2}\mu gt_0-(-\frac{3}{2}\mu gt_0)}{t_0}=2\mu g$，设小物块的质量为$m$，对小物块，由牛顿第二定律有$\mu'mg=ma'$，可得$\mu'=2\mu$，B正确；由$v-t$图像可知，$3t_0\sim4t_0$时间内，木板的加速度大小$a_2=\mu g$，对木板分析有$F-\mu'mg-\mu(M+m)g=-Ma_2$，可得$m:M=1:2$，C错误；$t=4t_0$之后，假设木板与小物块相对静止，对整体有$F-\mu(M+m)g=0$，假设成立，所以$t=4t_0$之后小物块与木板一起做匀速运动，D正确。

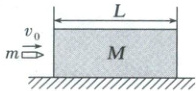
[例 2](多选)(2024·湖北卷)如图所示，在光滑水平面上静止放置一质量为$M$、长为$L$的木块，质量为$m$的子弹水平射入木块。设子弹在木块内运动过程中受到的阻力不变，其大小$f$与射入初速度大小$v_{0}$成正比，即$f = kv_{0}$($k$为已知常量)。改变子弹的初速度大小$v_{0}$，若木块获得的速度最大，则(AD)


A.子弹的初速度大小为$\frac{2kL(m + M)}{mM}$
B.子弹在木块中运动的时间为$\frac{2mM}{k(m + M)}$
C.木块和子弹损失的总动能为$\frac{k^{2}L^{2}(m + M)}{mM}$
D.木块在加速过程中运动的距离为$\frac{mL}{m + M}$

答案： 例2 答案：AD
解析：子弹在木块内运动的过程中，子弹与木块组成的系统所受合外力为0，所以该系统动量守恒，若子弹没有射出木块，则由动量守恒定律有$mv_0=(m+M)v$，解得木块获得的速度大小为$v=\frac{mv_0}{m+M}$，又子弹的初速度越大，其打入木块越深，则当子弹恰不射出木块时，木块获得的速度最大，此时有$\frac{1}{2}mv_0^2=\frac{1}{2}(m+M)v^2+kv_0L$，解得$v_0=\frac{2kL(m+M)}{mM}$；若子弹能够射出木块，则有$v_0＞\frac{2kL(m+M)}{mM}$，子弹在木块内运动的过程，对子弹和木块分别由牛顿第二定律有$kv_0=ma_m$，$kv_0=Ma_M$，根据位移关系有$v_0t-\frac{1}{2}a_mt^2-\frac{1}{2}a_Mt^2=L$，对木块有$v_M=a_Mt$，联立解得$v_M=\frac{2kmL}{2Mm-(M+m)kt}$，又$v_0$越大，穿出木块所需时间$t$越小，则$v_M$越小，即随着$v_0$的增大，木块获得的速度$v_M$不断减小。综上，若木块获得的速度最大，则子弹的初速度大小$v_0=\frac{2kL(m+M)}{mM}$，A正确；子弹在木块内运动的过程，对子弹由动量定理有$-kv_0t=mv-mv_0$，解得子弹在木块中运动的时间$t=\frac{mM}{k(m+M)}$，B错误；由能量守恒定律可知，木块和子弹损失的总动能$\Delta E_k=kv_0L=\frac{2k^2L^2(m+M)}{mM}$，C错误；木块在加速过程中做匀加速运动，由运动学规律有$x=\frac{v_Mt}{2}=\frac{mL}{m+M}$，D正确。

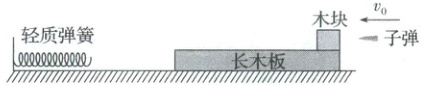
[例 3]（2025·山东·模拟预测）如图所示，长木板静止在光滑水平地面上，一木块（可视为质点）放置在长木板的最右端，一轻质弹簧固定在长木板左侧的竖直墙壁上。某一时刻子弹（可视为质点）以水平速度$v_{0}$射中木块并在极短时间内嵌入其中，之后二者一起运动，当木块与长木板达到共同速度$v_{共}=3m/s$时，长木板左端刚好与弹簧接触，之后长木板开始压缩弹簧，弹簧压缩至最短时，弹簧自锁（即不再压缩也不恢复形变），此时木块恰好停留在长木板的最左端。已知子弹的质量$m_{0}=10g$，木块的质量$m = 0.99kg$，长木板的质量$M = 1kg$，木块与长木板间的动摩擦因数$\mu = 0.2$，长木板的长度$l = 6.5m$，取$g = 10m/s^{2}$。求：

（1）子弹射入木块前的速度大小；
（2）开始时长木板左端与弹簧右端之间的距离；
（3）弹簧的最大弹性势能。

答案： 例3 答案：
(1)$600\ m/s$
(2)$2.25\ m$
(3)$5\ J$
解析：
(1)对子弹、木块和长木板三者组成的系统，根据动量守恒定律，有$m_0v_0=(m_0+m+M)v_共$解得$v_0=600\ m/s$。
(2)子弹射中木块的极短时间内，根据动量守恒定律，有$m_0v_0=(m_0+m)v'$解得$v'=6\ m/s$
长木板未接触弹簧前，木块在长木板上滑行时，对木块（含子弹），根据牛顿第二定律有$\mu(m_0+m)g=(m_0+m)a_1$解得$a_1=2\ m/s^2$
对长木板，根据牛顿第二定律有$\mu(m_0+m)g=Ma_2$解得$a_2=2\ m/s^2$
设长木板未接触弹簧前，木块与长木板发生相对滑行的时间为$t$，则根据运动规律有$v'-a_1t=a_2t$解得$t=1.5\ s$
此段时间内，木块的位移大小$x=v't-\frac{1}{2}a_1t^2=6.75\ m$
长木板的位移大小$d=\frac{1}{2}a_2t^2=2.25\ m$。
(3)长木板未接触弹簧前，木块相对于长木板的位移大小$\Delta x=x-d=4.5\ m$
长木板接触弹簧时，木块与长木板左端的距离$d'=l-\Delta x=2\ m$
长木板压缩弹簧的过程，对木块（含子弹）、长木板与弹簧组成的系统，根据能量守恒定律有$\frac{1}{2}(M+m+m_0)v_共^2=\mu(m+m_0)gd'+E_{pm}$
解得$E_{pm}=5\ J$。

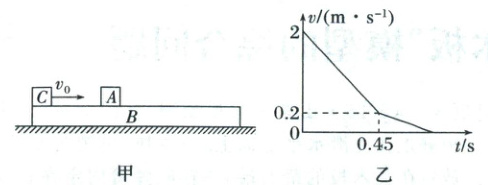
[例 4]（2025·河南郑州一模）如图甲所示，质量$m_{B}=3kg$的长木板$B$上表面放置一质量$m_{A}=2kg$的物块$A$，另有一质量$m_{C}=1kg$的物块$C$以某一初速度$v_{0}$从长木板最左端滑上长木板，物块$C$与物块$A$发生弹性碰撞后恰能从长木板左端滑落，物块$A$最终未从长木板滑离。物块$A$、$C$与长木板$B$之间的动摩擦因数均为$\mu_{1}$，长木板$B$与地面之间的动摩擦因数为$\mu_{2}$，两物块碰撞前长木板与地面相对静止。从两物块碰撞后瞬间开始计时，物块$A$的$v - t$图像如图乙所示，重力加速度$g$取$10m/s^{2}$。求：

（1）两物块碰撞后瞬间$C$的速度大小；
（2）动摩擦因数$\mu_{1}$、$\mu_{2}$的值；
（3）长木板$B$与地面之间由于摩擦产生的热量。

答案： 例4 答案：
(1)$1\ m/s$
(2)$0.4\ 0.1$
(3)$0.2\ J$
解析：
(1)规定向右为正方向，设两物块碰撞前瞬间$C$的速度为$v_C$，碰后瞬间$C$的速度为$v_C'$，碰后瞬间物块$A$的速度为$v_A$，物块$C$与物块$A$发生弹性碰撞，满足动量守恒和机械能守恒，则有
$m_Cv_C=m_Cv_C'+m_Av_A$
$\frac{1}{2}m_Cv_C^2=\frac{1}{2}m_Cv_C'^2+\frac{1}{2}m_Av_A^2$
解得$v_A=\frac{2m_C}{m_A+m_C}v_C=\frac{2}{3}v_C$
$v_C'=\frac{m_C-m_A}{m_A+m_C}v_C=-\frac{1}{3}v_C$
由乙图可知，物块$A$发生碰撞后速度$v_A=2\ m/s$
解得$v_C'=-1\ m/s$，负号表示方向向左。
(2)由乙图可知，$0\sim0.45\ s$内，$A$做匀减速直线运动的加速度大小为$a_A=\frac{\Delta v}{\Delta t}=4\ m/s^2$
由牛顿第二定律得$\mu_1m_Ag=m_Aa_A$
解得$\mu_1=0.4$
物块$C$从碰撞后到滑落过程中，设加速度大小为$a_C$，由牛顿第二定律得$\mu_1m_Cg=m_Ca_C$
解得$a_C=4\ m/s^2$
物块$C$恰好能从长木板左端滑落时速度为零，物块$C$从碰撞后到滑落的时间$t_1=\frac{0-v_C'}{a_C}=0.25\ s$
设物块$C$从长木板滑落后，长木板的加速度大小为$a_B$
有$\mu_1m_Ag-\mu_2(m_A+m_B)g=m_Ba_B$
由乙图可知$t_2=0.45\ s$后，物块$A$和长木板共速，速度大小是$v_A=v_B=0.2\ m/s$
由运动学公式得$v_B=a_B(t_2-t_1)$
解得$a_B=1\ m/s^2$，$\mu_2=0.1$。
(3)长木板$B$加速阶段的位移大小$x_1=\frac{v_B}{2}(t_2-t_1)$
解得$x_1=0.02\ m$
设从$A$、$B$共速到停止运动的加速度大小为$a$，位移大小为$x_2$，
有$\mu_2(m_A+m_B)g=(m_A+m_B)a$
$v_B^2=2ax_2$
解得$x_2=0.02\ m$
长木板$B$与地面之间由于摩擦产生的热量为
$Q=\mu_2(m_A+m_B)g(x_1+x_2)$
解得$Q=0.2\ J$。