2026年学易优高考二轮总复习物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年学易优高考二轮总复习物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. (2025·湖北武汉高三期末)一物体静止在光滑水平面上,从$t = 0$时刻起,受到的水平外力$F$作用,如图所示,以向右运动为正方向,物体质量为$2.5\,kg$,则下列说法正确的是(
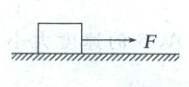
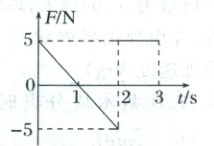
A.$t = 2\,s$时物体回到出发点
B.$t = 3\,s$时物体的速度大小为$1\,m/s$
C.前$2\,s$内物体的平均速度为$0$
D.第$3\,s$内物体的位移为$1\,m$
D
)

A.$t = 2\,s$时物体回到出发点
B.$t = 3\,s$时物体的速度大小为$1\,m/s$
C.前$2\,s$内物体的平均速度为$0$
D.第$3\,s$内物体的位移为$1\,m$
答案:
1 答案:D
解析:由题图知$\frac{1}{2}Ft - \frac{1}{2}Ft = 0$,$t = 2\ s$时物体速度变为$0$,没有回到原点,A错误;$0 \sim 3\ s$内,由动量定理知$\frac{1}{2}Ft - \frac{1}{2}Ft + Ft' = mv - 0$,解得$v = 2\ m/s$,B错误;前$2\ s$内物体位移不为$0$,由$\bar{v} = \frac{x}{t}$知平均速度不为$0$,C错误;第$3\ s$内物体做初速度为$0$的匀加速直线运动,位移$x = \frac{1}{2}at^{2} = \frac{1}{2} × \frac{5}{2.5} × 1^{2}\ m = 1\ m$,D正确。
解析:由题图知$\frac{1}{2}Ft - \frac{1}{2}Ft = 0$,$t = 2\ s$时物体速度变为$0$,没有回到原点,A错误;$0 \sim 3\ s$内,由动量定理知$\frac{1}{2}Ft - \frac{1}{2}Ft + Ft' = mv - 0$,解得$v = 2\ m/s$,B错误;前$2\ s$内物体位移不为$0$,由$\bar{v} = \frac{x}{t}$知平均速度不为$0$,C错误;第$3\ s$内物体做初速度为$0$的匀加速直线运动,位移$x = \frac{1}{2}at^{2} = \frac{1}{2} × \frac{5}{2.5} × 1^{2}\ m = 1\ m$,D正确。
2. (2025·黑龙江·模拟预测)大型工厂的车间中有一种设备叫做天车如图甲所示,是运输材料的一种常用工具。此装置可以简化为如图乙所示的模型,足够长的光滑水平杆上套有一个质量为$3m$的滑块,滑块正下方用长为$L$不可伸长的轻绳悬挂一个质量为$m$的小球。开始两者均静止,现给小球一个水平初速度$v_0$(未知),小球恰好能达到与滑块等高的位置,此时滑块水平向右移动$s$,重力加速度为$g$,求:
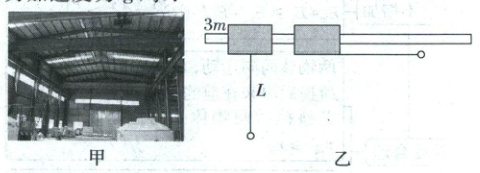
(1) 初速度$v_0$大小;
(2) 小球第$1$次返回最低点时绳的拉力大小;
(3) 从给小球初速度开始到第$1$次摆到最高点的时间。

(1) 初速度$v_0$大小;
(2) 小球第$1$次返回最低点时绳的拉力大小;
(3) 从给小球初速度开始到第$1$次摆到最高点的时间。
答案:
2.
(1)$v_{0} = \sqrt{\frac{8}{3}gL}$
(2)$F_{\mathrm{T}} = \frac{11}{3}mg$
(3)$t = \frac{4s + L}{4gL}\sqrt{6gL}$
解析:
(1)小球第一次到最高点时,小球和滑块达到相同速度,由水平方向的动量守恒$mv_{0} = 4mv_{共}$
由系统机械能守恒$\frac{1}{2}mv_{0}^{2} = \frac{1}{2} × 4mv_{共}^{2} + mgL$
联立得$v_{0} = \sqrt{\frac{8}{3}gL}$。
(2)小球第1次返回最低点时,设小球速度$v_{1}$,滑块的速度为$v_{2}$,对系统由动量守恒定律和机械能守恒定律$mv_{0} = mv_{1} + 3mv_{2}$,
$\frac{1}{2}mv_{0}^{2} = \frac{1}{2}mv_{1}^{2} + \frac{1}{2} × 3mv_{2}^{2}$
解得$v_{1} = -\frac{1}{2}v_{0}$,$v_{2} = \frac{1}{2}v_{0}$
由牛顿第二定律$F_{\mathrm{T}} - mg = \frac{m(v_{2} - v_{1})^{2}}{L}$
联立解得$F_{\mathrm{T}} = \frac{11}{3}mg$。
(3)从开始到第1次摆到最高点的过程中二者组成系统水平方向动量守恒,取极短时间$\Delta t$内
$mv_{0}\Delta t = mv_{1}\Delta t + 3mv_{2}\Delta t$
又$\sum v_{1}\Delta t = s_{1} = s + L$,$\sum v_{2}\Delta t = s_{2} = s$
则$mv_{0}t = ms_{1} + 3ms_{2}$
解得$t = \frac{4s + L}{v_{0}} = \frac{4s + L}{4gL}\sqrt{6gL}$。
(1)$v_{0} = \sqrt{\frac{8}{3}gL}$
(2)$F_{\mathrm{T}} = \frac{11}{3}mg$
(3)$t = \frac{4s + L}{4gL}\sqrt{6gL}$
解析:
(1)小球第一次到最高点时,小球和滑块达到相同速度,由水平方向的动量守恒$mv_{0} = 4mv_{共}$
由系统机械能守恒$\frac{1}{2}mv_{0}^{2} = \frac{1}{2} × 4mv_{共}^{2} + mgL$
联立得$v_{0} = \sqrt{\frac{8}{3}gL}$。
(2)小球第1次返回最低点时,设小球速度$v_{1}$,滑块的速度为$v_{2}$,对系统由动量守恒定律和机械能守恒定律$mv_{0} = mv_{1} + 3mv_{2}$,
$\frac{1}{2}mv_{0}^{2} = \frac{1}{2}mv_{1}^{2} + \frac{1}{2} × 3mv_{2}^{2}$
解得$v_{1} = -\frac{1}{2}v_{0}$,$v_{2} = \frac{1}{2}v_{0}$
由牛顿第二定律$F_{\mathrm{T}} - mg = \frac{m(v_{2} - v_{1})^{2}}{L}$
联立解得$F_{\mathrm{T}} = \frac{11}{3}mg$。
(3)从开始到第1次摆到最高点的过程中二者组成系统水平方向动量守恒,取极短时间$\Delta t$内
$mv_{0}\Delta t = mv_{1}\Delta t + 3mv_{2}\Delta t$
又$\sum v_{1}\Delta t = s_{1} = s + L$,$\sum v_{2}\Delta t = s_{2} = s$
则$mv_{0}t = ms_{1} + 3ms_{2}$
解得$t = \frac{4s + L}{v_{0}} = \frac{4s + L}{4gL}\sqrt{6gL}$。
查看更多完整答案,请扫码查看


