《2026年学易优高考二轮总复习物理》

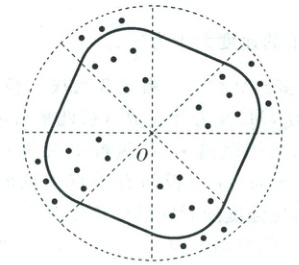
1. (多选)(2025·福建·二模)中国科学家利用兰州重离子加速器进行医用同位素的同步分离制备，“扇形聚焦回旋加速器”是该装置的重要构造部分。某种扇形聚焦磁场分布的简化图如图所示，圆心为 $O$ 的圆形区域等分成 8 个扇形区域，相互间隔的 4 个区域内存在方向垂直纸面向外、磁感应强度大小为 $B$ 的匀强磁场，另外 4 个区域内没有磁场。质量为 $m$、电荷量为 $q$ 的正离子以恒定速率在闭合平衡轨道上做周期性运动，其闭合平衡轨道如图中实线所示，离子重力不计，则离子绕闭合平衡轨道运动一周的过程中 (AD)


A.运动的方向是顺时针
B.运动的方向是逆时针
C.在磁场中运动的总时间为 $\frac{πm}{Bq}$
D.在磁场中运动的总时间为 $\frac{2πm}{Bq}$

答案： 高考预测
1.答案:AD
解析:由于粒子带正电，在磁场中由洛伦兹力提供向心力，根据左手定则可知，粒子运动的方向是顺时针，故A正确，B错误；因为粒子在没有磁场的区域做匀速直线运动，没有改变速度方向，则离子经过4个扇形磁场区域总共转过的角度为$360^{\circ}$，所以离子在磁场中运动的总时间等于离子在磁场中的运动周期，根据牛顿第二定律可得$qvB = m\frac{v^{2}}{r}$，又$T=\frac{2\pi r}{v}$，联立可得$T=\frac{2\pi m}{Bq}$，可知离子在磁场中运动的总时间为$\frac{2\pi m}{Bq}$，故C错误，D正确。 故选AD。

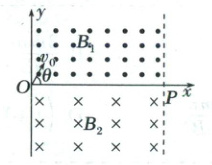
2. （2025·山西太原二模）一种能精准控制带电粒子运动轨迹和运动时间装置的原理如图所示。在 $xOy$ 平面内 $0 ＜ x ≤ 2\sqrt{3}L$ 的区域内，第一象限内存在方向垂直于纸面向外的匀强磁场，第四象限内存在方向垂直于纸面向里的匀强磁场，两磁场磁感应强度的大小关系为 $B_1 = 2B_2$。处于 $O$ 点的粒子源，能沿与 $x$ 轴成 $θ = 60°$ 角的方向，向第一象限发射质量为 $m$、带电荷量为 $q$、速度为 $v_0$ 的正粒子，粒子最终从 $x$ 轴上的 $P(2\sqrt{3}L, 0)$ 点射出磁场，不计粒子的重力。

(1) 求磁感应强度 $B_1$ 的最小值；
(2) 若 $B_1 = \frac{2mv_0}{qL}$，求粒子在磁场中通过的路程。

答案： 2.答案:
(1)$\frac{mv_{0}}{2qL}$
(2)$\frac{4}{3}\pi L$
解析:
(1)磁感应强度越小，轨迹圆半径就越大，$B_{0}$取最小值$B_{1min}$，粒子由$O$直接到达$P$，设粒子运动半径为$r_{1}$，则$qv_{0}B_{1min}=m\frac{v_{0}^{2}}{r_{1}}$
$2r_{1}\sin\theta = 2\sqrt{3}L$，解得$B_{1min}=\frac{mv_{0}}{2qL}$。
(2)若$B_{1}=\frac{2mv_{0}}{qL}＞B_{1min}$，粒子在第一象限及第四象限运动半径分别为$r_{2}$、$r_{3}$
则$qv_{0}B_{1}=m\frac{v_{0}^{2}}{r_{2}}$，$qv_{0}B_{2}=m\frac{v_{0}^{2}}{r_{3}}$
由几何关系知$n_{1}· 2r_{2}\sin\theta + n_{2}· 2r_{3}\sin\theta = 2\sqrt{3}L$
$(n_{1}=n_{2}$或$n_{1}=n_{2}+1)$
解得$r_{2}=\frac{L}{2}$，$r_{3}=L$，$n_{1}=2$，$n_{2}=1$
粒子在第一象限路程$s_{1}=n_{1}·\frac{1}{3}· 2\pi r_{2}$
粒子在第四象限路程$s_{2}=n_{2}·\frac{1}{3}· 2\pi r_{3}$
粒子在磁场中运动的路程$s=s_{1}+s_{2}$
解得$s_{1}=\frac{2}{3}\pi L$，$s_{2}=\frac{2}{3}\pi L$，$s=\frac{4}{3}\pi L$。