《2025年全校核心素养测评高中数学选择性必修第二册人教版》

1. 若函数 $ y = f(x) $ 可导，则“$ f'(x) = 0 $ 有实根”是“$ f(x) $ 有极值”的（ ）

A.必要不充分条件
B.充分不必要条件
C.充要条件
D.既不充分也不必要条件

答案： 1.A

2. (2024·江苏徐州高二期末)已知函数 $ f(x) $ 的定义域为 $ (a,b) $，导函数 $ f'(x) $ 的图象如图所示，则函数 $ f(x) $ 的极小值点的个数为（ ）


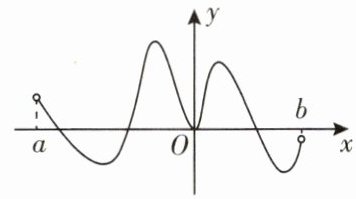
A.1
B.2
C.3
D.4

答案： 2.A

3. (2025·陕西榆林高二期末)已知函数 $ f(x) = xe^x $ 的极小值为（ ）

A.$e$
B.$-1$
C.$-e$
D.$-\dfrac{1}{e}$

答案： 3.D

4. 若函数 $ f(x) = x^3 - \left( \dfrac{a}{2} + 3 \right) x^2 + 2ax + 3 $ 在 $ x = 2 $ 处取得极小值，则实数 $ a $ 的取值范围是（ ）

A.$ (-\infty, -6) $
B.$ (-\infty, 6) $
C.$ (6, +\infty) $
D.$ (-6, +\infty) $

答案： 4.C

5. 若函数 $ y = e^x - 2mx $ 有小于零的极值点，则实数 $ m $ 的取值范围是（ ）

A.$ \left( -\infty, \dfrac{1}{2} \right) $
B.$ \left( 0, \dfrac{1}{2} \right) $
C.$ \left( \dfrac{1}{2}, +\infty \right) $
D.$ (0,1) $

答案： 5.B

6. 已知函数 $ f(x) = ax^3 + bx^2 + cx $ 的图象如图所示，且 $ f(x) $ 在 $ x = x_0 $ 与 $ x = 2 $ 处取得极值，则 $ f(1) + f(-1) $ 的值一定（ ）


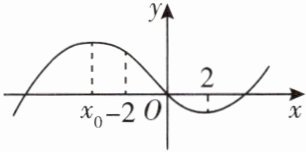
A.等于0
B.大于0
C.小于0
D.小于或等于0

答案： 6.C

7. 已知 $ f'(x) $ 是函数 $ f(x) $ 的导函数，若函数 $ y = e^{f'(x)} $ 的大致图象如图所示，则 $ f(x) $ 的极大值点为（ ）


A.$ a $
B.$ b $
C.$ c $
D.$ d $

答案： 7.B

8. (多选)已知函数 $ f(x) = x^3 + ax^2 + (a + 6) · x + 1 $ 有极大值和极小值，则实数 $ a $ 的值可以是（ ）

A.$-4$
B.$-3$
C.$6$
D.$8$

答案： 8.AD

9. (多选)(2024·福建南平高二月考)已知函数 $ f(x) $ 的导函数为 $ f'(x) = ax^2 - 2ax (a \neq 0) $，则函数 $ f(x) $ 的图象可能是（ ）

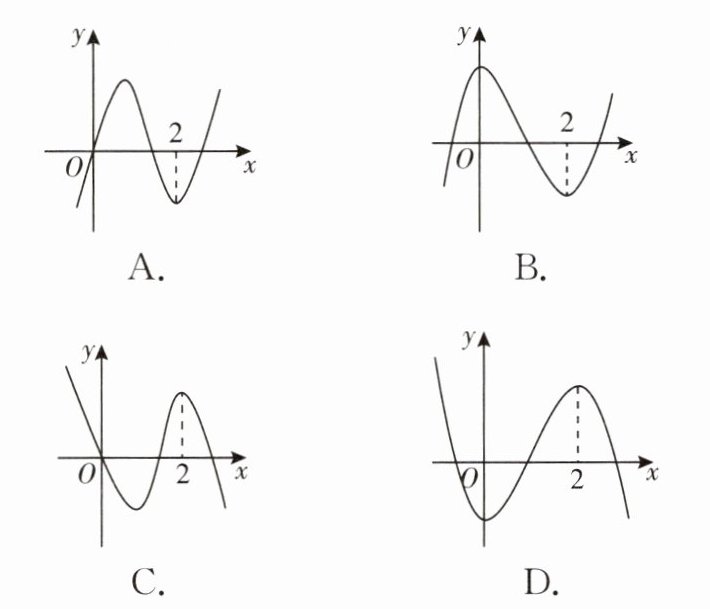
答案： 9.AC

10. 设 $ x = 1 $ 与 $ x = 2 $ 是函数 $ f(x) = a\ln x + bx^2 + x $ 的两个极值点，则常数 $ a = $______.

答案： 10. $-\dfrac{2}{3}$

11. 若函数 $ f(x) = \dfrac{1}{3}x^3 + (a - 1)x^2 + x + 1 $ 没有极值，则实数 $ a $ 的取值范围是______.

答案： 11. $[0,2]$