《2025年全校核心素养测评高中数学选择性必修第二册人教版》

9. （多选）八年来，甲工厂某种产品年产量 $ y $ 与时间 $ x $（单位：年）的函数关系如图所示。下列说法中，正确的是（ ）


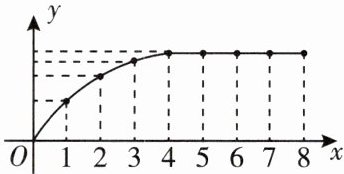
A.前四年该产品产量增长速度越来越快
B.前四年该产品产量增长速度越来越慢
C.第四年后该产品停止生产
D.第四年后该产品年产量保持不变

答案： 9.BD

10. 若抛物线 $ f(x) = 4x^2 $ 在点 $ (x_0,f(x_0)) $ 处切线的斜率为 $ 8 $，则 $ x_0 = $________。

答案： 10.1

11. 一物体的运动方程为 $ s = 7t^2 + 8 $，则其初速度为________，其在 $ t = $________时的瞬时速度为 $ 1 $。

答案： 11.0；$\frac{1}{14}$

12. 已知定义在 $ \mathbf{R} $ 上的函数 $ f(x) = ax^2 - 2x - 1 $，且曲线 $ y = f(x) $ 在点 $ (1,f(1)) $ 处的切线斜率为 $ 4 $，则 $ a = $________。

答案： 12.3

13. 某飞行器发射后的一段时间内，时间 $ t $ 与飞行器高度 $ h $ 的关系为 $ h(t) = 5t^3 + 30t^2 + 45t + 4 $，其中 $ h $ 的单位为 $ m $，$ t $ 的单位为 $ s $。
(1) $ h(0) $，$ h(1) $ 分别表示什么？
(2) 求 $ t = 0 \, s $ 到 $ t = 1 \, s $ 这段时间内飞行器的平均速度。
(3) 求 $ t = 1 \, s $ 时飞行器的瞬时速度。

答案： 13.解：
(1)$h(0)$表示飞行器发射时的高度，$h(1)$表示飞行器发射1s后的高度。
(2)$\because h(0)=4$，$h(1)=5+30+45+4=84$，$\therefore$从$t=0s$到$t=1s$这段时间内飞行器的平均速度为$\frac{h(1)-h(0)}{1-0}=80m/s$。
(3)$\because\Delta h=h(1+\Delta t)-h(1)=5(1+\Delta t)^3+30(1+\Delta t)^2+45(1+\Delta t)+4-84=5[1+3\Delta t+3(\Delta t)^2+(\Delta t)^3]+30[1+2\Delta t+(\Delta t)^2]+45+45\Delta t+4-84=5+15\Delta t+15(\Delta t)^2+5(\Delta t)^3+30+60\Delta t+30(\Delta t)^2+45+45\Delta t+4-84=120\Delta t+45(\Delta t)^2+5(\Delta t)^3$，$\therefore\frac{\Delta h}{\Delta t}=120+45\Delta t+5(\Delta t)^2$，$\therefore$当$\Delta t\to0$时，$\frac{\Delta h}{\Delta t}\to120$，即$t=1s$时飞行器的瞬时速度为$120m/s$。

14. 曲线 $ y = x^2 $ 在哪一点处的切线分别满足下列条件？
(1) 平行于直线 $ y = 4x - 5 $；
(2) 垂直于直线 $ 2x - 6y + 5 = 0 $；
(3) 倾斜角为 $ 135° $。

答案： 14.解：设曲线$y=x^2$在点$(x_0,y_0)$处的切线满足条件。
(1)切线平行于直线$y=4x-5$，$\therefore$切线斜率$k=4$。$\because y'=\lim_{\Delta x\to0}\frac{(x_0+\Delta x)^2-x_0^2}{\Delta x}=\lim_{\Delta x\to0}(2x_0+\Delta x)=2x_0$，$\therefore2x_0=4$，$\therefore x_0=2$，$\therefore y_0=4$，即曲线在点$(2,4)$处的切线平行于直线$y=4x-5$。
(2)切线垂直于直线$2x-6y+5=0$，$\because$直线$2x-6y+5=0$的斜率为$\frac{1}{3}$，$\therefore$切线斜率$k=-3$，$\therefore2x_0=-3$，$\therefore x_0=-\frac{3}{2}$，$\therefore y_0=\left(-\frac{3}{2}\right)^2=\frac{9}{4}$，即曲线在点$\left(-\frac{3}{2},\frac{9}{4}\right)$处的切线垂直于直线$2x-6y+5=0$。
(3)切线倾斜角为$135°$，$\therefore$切线斜率$k=\tan135°=-1$，$\therefore2x_0=-1$，$\therefore x_0=-\frac{1}{2}$，$\therefore y_0=\left(-\frac{1}{2}\right)^2=\frac{1}{4}$，即曲线在点$\left(-\frac{1}{2},\frac{1}{4}\right)$处的切线倾斜角为$135°$。

15. 将半径为 $ R $ 的球加热，若半径从 $ R = 1 $ 到 $ R = m $ 时球的体积膨胀率为 $ \frac{28\pi}{3} $，则 $ m $ 的值为________。

答案： 15.3

16. 若一物体运动方程如下（位移单位：$ m $，时间单位：$ s $）：
$ s = f(t) = \begin{cases} 3t^2 + 2, & t \geq 3, \\ 29 + 3(t - 3)^2, & 0 \leq t ＜ 3. \end{cases} $
求：(1) 物体在 $ t \in [3,5] $ 内的平均速度；
(2) 物体的初速度 $ v_0 $；
(3) 物体在 $ t = 1 $ 时的瞬时速度。

答案： 16.解：
(1)$\because$物体在$t\in[3,5]$内的时间变化量为$\Delta t=5-3=2$，位移变化量为$\Delta s=3×5^2+2-(3×3^2+2)=3×(25-9)=48$，$\therefore$物体在$t\in[3,5]$内的平均速度为$\frac{\Delta s}{\Delta t}=\frac{48}{2}=24m/s$。
(2)求物体的初速度$v_0$，即求物体在$t=0$时的瞬时速度。$\because$当$0\leq t＜3$时，$s=29+3(t-3)^2=3t^2-18t+56$，$\Delta s=3(0+\Delta t)^2-18(0+\Delta t)+56-(0-0+56)=3(\Delta t)^2-18\Delta t$，$\therefore\frac{\Delta s}{\Delta t}=3\Delta t-18$，$\therefore$物体在$t=0$处的瞬时速度为$\lim_{\Delta t\to0}\frac{\Delta s}{\Delta t}=\lim_{\Delta t\to0}(3\Delta t-18)=-18m/s$，即物体的初速度$v_0=-18m/s$。
(3)物体在$t=1$时的瞬时速度，即求当$t=1$时的瞬时速度。$\because$当$0\leq t＜3$时，$s=3t^2-18t+56$，$\Delta s=3(1+\Delta t)^2-18(1+\Delta t)+56-(3-18+56)=3[1+2\Delta t+(\Delta t)^2]-18-18\Delta t+56-41=3+6\Delta t+3(\Delta t)^2-18-18\Delta t+56-41=3(\Delta t)^2-12\Delta t$，$\therefore\frac{\Delta s}{\Delta t}=3\Delta t-12$，$\therefore$物体在$t=1$时的瞬时速度为$\lim_{\Delta t\to0}\frac{\Delta s}{\Delta t}=\lim_{\Delta t\to0}(3\Delta t-12)=-12m/s$。