2025年全校核心素养测评高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年全校核心素养测评高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
10. 已知数列$\{ a_{n}\}$的通项公式$a_{n}=\frac{n}{n + 1}$,则$a_{n}· a_{n + 1}· a_{n + 2}=$________.
答案:
10. $\frac{n}{n + 3}$
11. (2024·重庆三中高二月考)已知数列$\{ a_{n}\}$满足$a_{n}=2n^{2}+\lambda n + 3,n\in\mathbf{N}^{*}$,且$\{ a_{n}\}$是递增数列,则实数$\lambda$的取值范围是________.
答案:
11. $(-6,+\infty)$
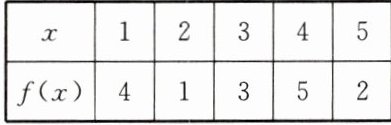
12. 已知函数$f(x)$的定义如表所示,数列$\{ x_{n}\}$满足$x_{0}=5$,且对任意的自然数均有$x_{n + 1}=f(x_{n})$,则$x_{2023}=$________.

答案:
12. 2
13. 写出下列各数列的一个通项公式:
(1)4,6,8,10,…;
(2)$\frac{1}{2},\frac{3}{4},\frac{7}{8},\frac{15}{16},\frac{31}{32},·s$;
(3)$-1,\frac{8}{5},-\frac{15}{7},\frac{24}{9},·s$.
(1)4,6,8,10,…;
(2)$\frac{1}{2},\frac{3}{4},\frac{7}{8},\frac{15}{16},\frac{31}{32},·s$;
(3)$-1,\frac{8}{5},-\frac{15}{7},\frac{24}{9},·s$.
答案:
13. 解:(1)各项是从4开始的偶数,所以$a_n=2n+2$。
(2)每一项的分子比分母少1,而分母组成数列$2^1,2^2,2^3,2^4,·s$,所以$a_n=\frac{2^n-1}{2^n}$。
(3)奇数项为负,偶数项为正,故通项公式中含因式$(-1)^n$;各项绝对值的分母组成数列3,5,7,9,$·s$,即$\{2n+1\}$;而各项绝对值的分子组成的数列中,奇数项为1=1×1,偶数项为8=2×4,15=3×5,24=4×6,可表示为$n(n+2)$,所以$a_n=(-1)^n·\frac{n(n+2)}{2n+1}$。
(2)每一项的分子比分母少1,而分母组成数列$2^1,2^2,2^3,2^4,·s$,所以$a_n=\frac{2^n-1}{2^n}$。
(3)奇数项为负,偶数项为正,故通项公式中含因式$(-1)^n$;各项绝对值的分母组成数列3,5,7,9,$·s$,即$\{2n+1\}$;而各项绝对值的分子组成的数列中,奇数项为1=1×1,偶数项为8=2×4,15=3×5,24=4×6,可表示为$n(n+2)$,所以$a_n=(-1)^n·\frac{n(n+2)}{2n+1}$。
14. 已知数列$\{ a_{n}\}$中,$a_{1}=3$,$a_{10}=21$,$a_{n}$是关于项数$n$的一次函数.
(1)求$\{ a_{n}\}$的通项公式,并求$a_{2023}$;
(2)若数列$\{ b_{n}\}$是由$a_{2}$,$a_{4}$,$a_{6}$,$a_{8}$,…组成的,试归纳$\{ b_{n}\}$的一个通项公式.
(1)求$\{ a_{n}\}$的通项公式,并求$a_{2023}$;
(2)若数列$\{ b_{n}\}$是由$a_{2}$,$a_{4}$,$a_{6}$,$a_{8}$,…组成的,试归纳$\{ b_{n}\}$的一个通项公式.
答案:
14. 解:(1)设$a_n=kn+b$($k\neq0$),由题意得$\begin{cases}k+b=3,\\10k+b=21,\end{cases}$解得$\begin{cases}k=2,\\b=1.\end{cases}$
$\therefore a_n=2n+1$($n\in\mathbf{N}^*$),$\therefore a_{2023}=2×2023+1=4047$。
(2)$a_2=5$,$a_4=9$,$a_6=13$,$a_8=17$,即$b_1=5$,$b_2=9$,$b_3=13$,$b_4=17$,归纳得$b_n=4n+1$。
$\therefore a_n=2n+1$($n\in\mathbf{N}^*$),$\therefore a_{2023}=2×2023+1=4047$。
(2)$a_2=5$,$a_4=9$,$a_6=13$,$a_8=17$,即$b_1=5$,$b_2=9$,$b_3=13$,$b_4=17$,归纳得$b_n=4n+1$。
15. 函数$f(x)=\begin{cases}(3 - a)x - 3,x\leqslant7,\\a^{x - 6},x>7,\end{cases}$若数列$\{ a_{n}\}$满足$a_{n}=f(n),n\in\mathbf{N}^{*}$,且$\{ a_{n}\}$是递增数列,则实数$a$的取值范围是( )
A.$\frac{9}{4},3)$
B.$(\frac{9}{4},3)$
C.(1,3)
D.(2,3)
A.$\frac{9}{4},3)$
B.$(\frac{9}{4},3)$
C.(1,3)
D.(2,3)
答案:
15. D
16. 已知数列$\{ a_{n}\}$的通项公式为$a_{n}=\frac{n^{2}}{2^{n}}(n\in\mathbf{N}^{*})$,则这个数列是否存在最大项?若存在,请求出最大项;若不存在,请说明理由.
答案:
16. 解:存在最大项。理由如下:
假设第$n$项$a_n$为最大项,则$\begin{cases}a_n\geq a_{n-1},\\a_n\geq a_{n+1}\end{cases}$($n\geq2$),
即$\begin{cases}\frac{n^2}{2^n}\geq\frac{(n-1)^2}{2^{n-1}},\frac{n^2}{2^n}\geq\frac{(n+1)^2}{2^{n+1}},\end{cases}$
解得$\begin{cases}n^2\geq2(n-1)^2,\\2n^2\geq(n+1)^2,\end{cases}$
即$\begin{cases}n^2-4n+2\leq0,\\n^2-2n-1\geq0,\end{cases}$
解得$\begin{cases}2-\sqrt{2}\leq n\leq2+\sqrt{2},\\n\geq1+\sqrt{2}或n\leq1-\sqrt{2}.\end{cases}$
$\because n\in\mathbf{N}^*$,$\therefore n=3$,
$\therefore$最大项为$a_3=\frac{9}{8}$。
假设第$n$项$a_n$为最大项,则$\begin{cases}a_n\geq a_{n-1},\\a_n\geq a_{n+1}\end{cases}$($n\geq2$),
即$\begin{cases}\frac{n^2}{2^n}\geq\frac{(n-1)^2}{2^{n-1}},\frac{n^2}{2^n}\geq\frac{(n+1)^2}{2^{n+1}},\end{cases}$
解得$\begin{cases}n^2\geq2(n-1)^2,\\2n^2\geq(n+1)^2,\end{cases}$
即$\begin{cases}n^2-4n+2\leq0,\\n^2-2n-1\geq0,\end{cases}$
解得$\begin{cases}2-\sqrt{2}\leq n\leq2+\sqrt{2},\\n\geq1+\sqrt{2}或n\leq1-\sqrt{2}.\end{cases}$
$\because n\in\mathbf{N}^*$,$\therefore n=3$,
$\therefore$最大项为$a_3=\frac{9}{8}$。
查看更多完整答案,请扫码查看


